Solidity 中的对数计算
背景
在进行 solidity 开发时,某些场景可能需要进行对数的计算。对数计算虽然在通用编程领域已经有成熟的解决方案(几乎所有编程语言都有相关的内置库或者第三方库来实现)。但是在 solidity 中没有 floating/fixed point number(fixed point number 在 solidity 0.8 版本中仍处于 not fully supported 阶段)的支持,又缺乏这类计算的标准实现。因此在项目的开发中,可能会根据各自的需求,完成不同的实现。
本文尝试解释对数计算的步骤,并以实际项目代码(ABDK Library 和 Uniswap v3)为例进行解析。
计算步骤
预热
我们需要先熟悉以下对数公式的变化形式:
$$ log_b(x \cdot y) = log_bx + log_by \\ log_b{x^y} = y \cdot log_bx $$以及对数的换底公式:
$$ log_bx = \frac{log_nx}{log_nb} \\ log_bx = log_nx \times log_bn $$将计算转换为以 2 为底的计算
在进行对数计算时,我们可以先利用换底公式,将计算转换为 $log_2x$ 的计算:
$$ log_bx = \frac{log_2x}{log_2b} = log_2x \cdot log_b2 $$
这样做的原因是,可以将任意数为底的计算转换为以 2 为底的计算,在计算机中对 2 进制的位操作可以方便的进行 $log_2x$ 的计算。
$log_2x$ 的计算
整数部分
我们假设 $x$ 的的二进制表示中最高位位数为第 n 位(从 0 开始)。那么可以知道:
$$ 2^n \le x < 2^{n+1} $$
因此:
$$ n \le log_2x < n+1 $$
即我们要求的对数 $log_2x$ 的整数部分为 n. 那么我们只需要找出 $x$ 的最高位(Most Significant Bit, MSB)的位数,就求出了 $log_2x$ 结果的整数部分。
MSB 计算
关于 MSB 位数的计算,有多种实现方式:
- 按位迭代,时间复杂度为 O(n)
- 二分查找,时间复杂度为 O(logn)
- 使用德布鲁因序列(DeBruijn sequence)作为 hash table 来进行查找,时间复杂度为 O(1),空间复杂度为 O(n),参考:Bit Twiddling Hacks
在 solidity 开发中,我们既需要考虑时间复杂度,也需要考虑空间复杂度(memory 或 storage 操作都是耗费 gas 的操作),因此大家都比较偏好使用第二种方式来计算 MSB 位数。
这不再给出具体的代码实现,后文会参照真实项目的实现来进行讲解。
小数的表示
在计算机中,我们一般使用浮点或者定点数来表示一个小数 x:
$$ x = m \times 2^e $$
在存储时只需要存储尾数(mantissa) m 和指数(exponent) e 即可,并且这两个数都是以整数的形式存储的,一般来说指数 e 以负数的方式存储。
在使用定点数时,由于指数是固定的,那么只需要存储 m 的值即可。以 64 位定点数为例:
$$ x = m \times 2^{-64} $$
在计算 x 的对数时,计算其尾数的对数 $log_2m$ 即可:
$$ log_2(m \times 2^e) = log_2m + log_2{2^e} = log_2m + e (定点数对数公式) $$
求对数的小数部分
前面说到可以通过 MSB 求出对数结果的整数部分 n,求出整数部分 n 的值之后,需要求出小数部分的结果,小数部分即为:
$$ log_2x - n = log_2x - log_2{2^n} = log_2{\frac{x}{2^n}} $$
并且:
$$ \begin{cases} 0 \le log_2{\frac{x}{2^n}} < 1 \\ 1 \le \frac{x}{2^n} < 2 \end{cases} $$那么 $log_2{\frac{x}{2^n}}$ 就是对数结果的小数部分的值。先通过 $x := \frac{x}{2^n}$ 重新赋值将前面的公式简化为 $log_2x$,之后可以可以通过如下公式来对其进行转换:
$$ log_2x = \frac{log_2{x^2}}{2} \ \ \ \ \ \ \ \ (式1) \\ log_2x = 1 + log_2\frac{x}{2} \ \ \ \ (式2) $$注意,在使用式二进行转换时,式中加法的右边部分,需要保证 $\frac{x}{2} \ge 1$,否则 $log_2\frac{x}{2}$ 的值将会为负数,导致计算难度增大。
因为前面限定了条件 $1 \le x < 2$,那么我们可以把 $log_2x$ 的计算转化成以下形式:
$$ \begin{cases} log_2x = n_0 \times 1 + n_1 \times \frac{1}{2} + n_2 \times \frac{1}{4} + n_3 \times \frac{1}{8} + ... \\ n_i \in \{0, 1\} \end{cases} $$因为 $log_2x < 1$,这里可以省略掉 $n_0 \times 1$,即:
$$ \begin{cases} log_2x = n_1 \times \frac{1}{2} + n_2 \times \frac{1}{4} + n_3 \times \frac{1}{8} + ... \\ n_i \in \{0, 1\} \end{cases} $$即
$$ \begin{cases} log_2x = \sum_{i=1}^{\infty}{\frac{n_i}{2^i}} \\ n_i \in \{0, 1\} \end{cases} $$这样我们就把对数的计算转换成为了加法计算,加法计算迭代的次数越多,计算结果的精度就越高。
注意:上述公式中 $n_i$ 取值只能是 0 或者 1.
而判断 $n_i$ 值的方式需要迭代进行,假设我们迭代 100 次,使用 python 代码可以表示为:
def get_n_values(x):
assert 1 <= x < 2
n_list = [0] * 100
for i in range(0, 100):
if x >= 2: # 当 x>= 2 时,其 log2 的结果为正,可以使用公式 2 展开
n_list[i] = 1 # 使用公式2,这里求的是 n_i 的值
x /= 2 # 使用公式2
x *= x # 使用公式1
return n_list
上面的代码求出给定 x(1 ≤ x < 2),前 100 个 $n_i$ 的值。既然求出了 $n_i$ 的值,其实我们就可以直接求出结果了,改造上面的代码,我们将迭代次数也作为参数传入:
def log2(x, n):
assert 1 <= x < 2
result = 0
for i in range(0, n):
if x >= 2:
result += 1 / (2 ** i) # 使用公式2
x /= 2 # 使用公式2
x *= x # 使用公式1
return result
运行代码检验一下:
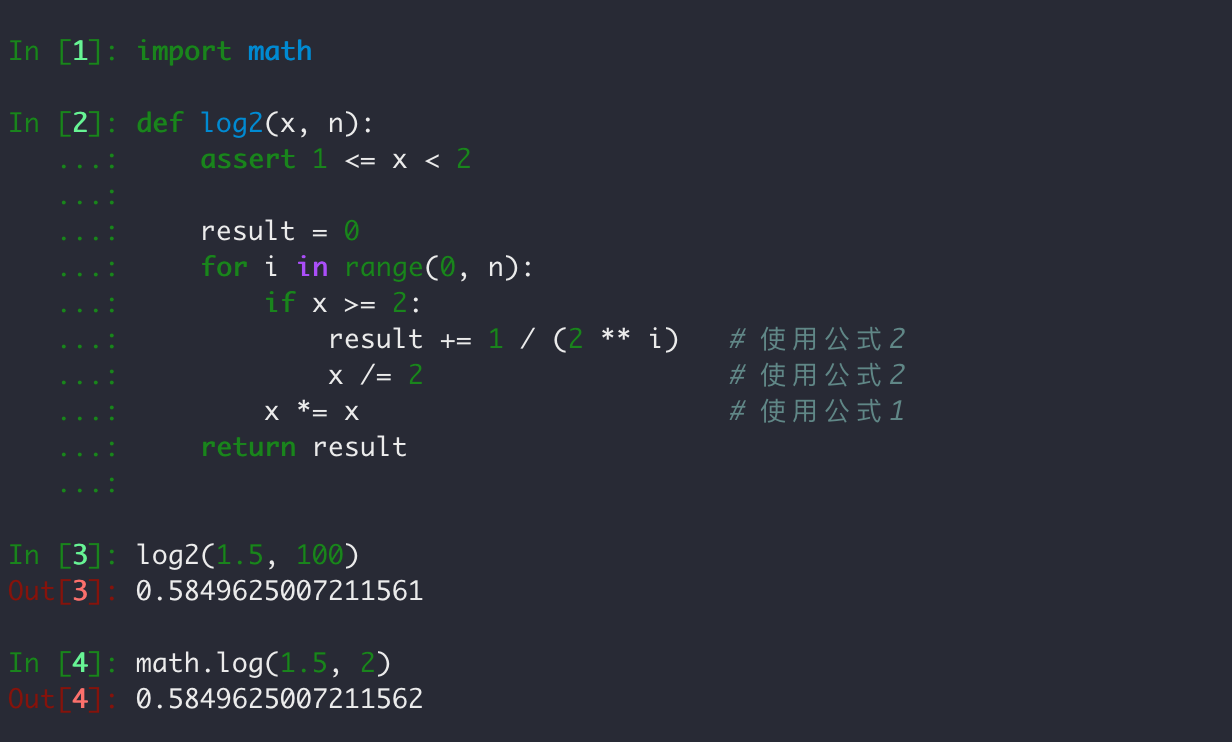
上述代码中每迭代一次,二进制的小数表示的对数结果就精确一位,可以看到运行的结果已经很精确了,但是这里我们偷懒使用了 python 内置的浮点数来进行分数的加法运算。
在 solidity 中,往往需要自己实现定点数,并基于此定点数来进行对数的计算。在后文,我会使用开源项目中的代码来进行分析 solidity 中的实现。
通用对数计算
计算任意底数的对数时,通过对数的计算都可以通过换底公式,转换为 $log_2x$ 的计算。例如:
$$ log_{b}x = \frac{log_2x}{log_2{b}} $$
如果是 $log_{10}x$ 或者 $lnx$ 这类常见的对数计算,可以通过事先计算好 $log_{10}2$, $ln2$ 的方式,直接通过 magic number 来进一步优化计算的实现。
solidity 中的实现
ABDK Library
ABDK Library 中实现了 Signed 64.64 fixed point number,使用 63 位整数位和 64 位的小数位,以及 1 位符号位。
代码中支持了 log_2 和 ln 的计算。本文参考代码链接为:ABDK Library
log2
log2 的代码实现为:
function log_2 (int128 x) internal pure returns (int128) {
unchecked { // 代码使用了 solidity 0.8,关闭溢出保护
require (x > 0);
int256 msb = 0;
int256 xc = x;
if (xc >= 0x10000000000000000) { xc >>= 64; msb += 64; }
if (xc >= 0x100000000) { xc >>= 32; msb += 32; }
if (xc >= 0x10000) { xc >>= 16; msb += 16; }
if (xc >= 0x100) { xc >>= 8; msb += 8; }
if (xc >= 0x10) { xc >>= 4; msb += 4; }
if (xc >= 0x4) { xc >>= 2; msb += 2; }
if (xc >= 0x2) msb += 1; // No need to shift xc anymore
// 上面的部分,通过二分查找的方式,求出 MSB 的位数
int256 result = msb - 64 << 64; // 将 MSB 的位数写入结果的整数部分,这里用到了前面的定点数对数公式
// 这里是求出 x/2^n, 并且将其整体左位移 127 位,位移后小数部分位数为 127 位
uint256 ux = uint256 (int256 (x)) << uint256 (127 - msb);
// 开始迭代,0x8000000000000000 即为 Q64.64 表示的 1/2,迭代的次数为 64 次
for (int256 bit = 0x8000000000000000; bit > 0; bit >>= 1) {
ux *= ux; // 计算 x^2,计算完成后小数部分位数为 254 位,整数部分为 2 位
uint256 b = ux >> 255; // 这里的 trick 是判断 ux >= 2,因为整数部分为 2 位,当 ux >= 2 时,其第 1 位必然为 1,第 0 位的值我们不需要关心
ux >>= 127 + b; // 将 ux 的小数部分恢复为 127 位,并且如果上一步中整数部分第 1 位为1,即 ux >= 2 时, ux = ux/2
result += bit * int256 (b); // 当 ux >= 2 时,将 delta 加到结果中
}
return int128 (result);
}
}
我们分解来看:
int256 msb = 0;
int256 xc = x;
if (xc >= 0x10000000000000000) { xc >>= 64; msb += 64; }
if (xc >= 0x100000000) { xc >>= 32; msb += 32; }
if (xc >= 0x10000) { xc >>= 16; msb += 16; }
if (xc >= 0x100) { xc >>= 8; msb += 8; }
if (xc >= 0x10) { xc >>= 4; msb += 4; }
if (xc >= 0x4) { xc >>= 2; msb += 2; }
if (xc >= 0x2) msb += 1; // No need to shift xc anymore
这一段通过二分查找的方式,求出了 MSB 的位数(整数),这个值就是我们要求的对数结果的整数部分。
求出整数部分之后,将其写到 result 中:
int256 result = msb - 64 << 64;
这里用了前面提到的定点数对数公式 $log_2(m \times 2^{-64}) = log_2m + log_2{2^{-64}} = log_2m - 64$,因为 result 是一个 Q64.64 定点数,需要将其左移 64 位。需要注意的是 solidity 中 << 运算符的优先级和其他常见编程语言不一样,上面两个运算符是从左至右的顺序执行的。
之后需要开始计算结果的小数部分,参照前面的公式,小数部分即为 $log_2\frac{x}{2^n}$,那么这里需要先计算出 $\frac{x}{2^n}$:
uint256 ux = uint256 (int256 (x)) << uint256 (127 - msb);
$\frac{x}{2^n}$ 可以通过 x >> n 来计算,这里再进行左移 127 位之后,上面的数成为了一个 Q129.127 的定点数,这样做的目的是为了后面方便 $x^2$ 与 2 进行大小比较。
计算完成后,开始进行迭代计算,计算方式和之前的 python 实现基本相同:
for (int256 bit = 0x8000000000000000; bit > 0; bit >>= 1) {
ux *= ux;
uint256 b = ux >> 255;
ux >>= 127 + b;
result += bit * int256 (b);
}
这里迭代的起始是从 0x8000000000000000 开始的,这个数是 Q64.64 表示的 1/2,每次迭代都会将其除以 2,直至其为 0. 那么对于 Q64 的定点数来说,迭代的次数为 64 次。
ux *= ux 计算了 x^2,并使得 ux 成为了一个 Q2.254 的定点数,这样这个数的整数部分只有 00, 01, 10, 11 四种可能。当 x^2 >= 2 时,其整数位第 1 位必为 1.
uint256 b = ux >> 255,b 即为 ux 整数位第 1 位的值,当其为 1 时,ux >= 2.
ux >>= 127 + b,右移 127 位将 ux 恢复为 Q129.127 定点数,如果前一步中计算的 b == 1 时,这里继续右移 1 位来计算 ux = ux / 2.
当 ux >= 2 时,将结果与 bit 相加,并且在进行下一次迭代之前,bit = bit / 2.
ln
有了 log2 的计算实现,ln 的计算就简单很多了,根据公式:
$$ lnx = log_2x \times ln2 $$
ABDK 中的实现如下:
function ln (int128 x) internal pure returns (int128) {
unchecked {
require (x > 0);
return int128 (int256 (
uint256 (int256 (log_2 (x))) * 0xB17217F7D1CF79ABC9E3B39803F2F6AF >> 128));
}
}
这里的 magic number 0xB17217F7D1CF79ABC9E3B39803F2F6AF 就是 ln2 << 128 的值。
Uniswap v3
在 Uniswap v3 中,tick 相关的计算也涉及到了对数的计算,价格 $P$ 与 tick index i 的关系为:
$$ \sqrt{P} = \sqrt{1.0001}^i $$
当给定价格 $\sqrt{P}$ 时,需要计算出 i 的值,即计算 $log_{\sqrt{1.0001}}x$ 的结果,因为 i 为整数,这里需要将对数结果向下或向上取整,得出 i 的值。
有人可能就会有疑问了,既然 i 为整数,那么是不是可以完全不需要想前面那样计算 log2 的小数部分?
答案是否定的,我们回顾一下公式:
$$ log_{\sqrt{1.0001}}x = log_2x \times log_{\sqrt{1.0001}}2 $$
如果不求 $log_2x$ 的小数部分,在进行上面的乘法时,会因为放大效应,而导致最终的计算结果可能出现比较大的误差(大于1)。
代码实现
Uniswap v3 的代码实现在:TickMath.sol
函数 getTickAtSqrtRatio(uint160 sqrtPriceX96) 求出给定 $\sqrt{P}$ 对应的 tick index i 的值。代码如下:
function getTickAtSqrtRatio(uint160 sqrtPriceX96) internal pure returns (int24 tick) {
// second inequality must be < because the price can never reach the price at the max tick
require(sqrtPriceX96 >= MIN_SQRT_RATIO && sqrtPriceX96 < MAX_SQRT_RATIO, 'R');
uint256 ratio = uint256(sqrtPriceX96) << 32;
uint256 r = ratio;
uint256 msb = 0;
assembly {
let f := shl(7, gt(r, 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF))
msb := or(msb, f)
r := shr(f, r)
}
assembly {
let f := shl(6, gt(r, 0xFFFFFFFFFFFFFFFF))
msb := or(msb, f)
r := shr(f, r)
}
assembly {
let f := shl(5, gt(r, 0xFFFFFFFF))
msb := or(msb, f)
r := shr(f, r)
}
assembly {
let f := shl(4, gt(r, 0xFFFF))
msb := or(msb, f)
r := shr(f, r)
}
assembly {
let f := shl(3, gt(r, 0xFF))
msb := or(msb, f)
r := shr(f, r)
}
assembly {
let f := shl(2, gt(r, 0xF))
msb := or(msb, f)
r := shr(f, r)
}
assembly {
let f := shl(1, gt(r, 0x3))
msb := or(msb, f)
r := shr(f, r)
}
assembly {
let f := gt(r, 0x1)
msb := or(msb, f)
}
if (msb >= 128) r = ratio >> (msb - 127);
else r = ratio << (127 - msb);
int256 log_2 = (int256(msb) - 128) << 64;
assembly {
r := shr(127, mul(r, r))
let f := shr(128, r)
log_2 := or(log_2, shl(63, f))
r := shr(f, r)
}
assembly {
r := shr(127, mul(r, r))
let f := shr(128, r)
log_2 := or(log_2, shl(62, f))
r := shr(f, r)
}
assembly {
r := shr(127, mul(r, r))
let f := shr(128, r)
log_2 := or(log_2, shl(61, f))
r := shr(f, r)
}
assembly {
r := shr(127, mul(r, r))
let f := shr(128, r)
log_2 := or(log_2, shl(60, f))
r := shr(f, r)
}
assembly {
r := shr(127, mul(r, r))
let f := shr(128, r)
log_2 := or(log_2, shl(59, f))
r := shr(f, r)
}
assembly {
r := shr(127, mul(r, r))
let f := shr(128, r)
log_2 := or(log_2, shl(58, f))
r := shr(f, r)
}
assembly {
r := shr(127, mul(r, r))
let f := shr(128, r)
log_2 := or(log_2, shl(57, f))
r := shr(f, r)
}
assembly {
r := shr(127, mul(r, r))
let f := shr(128, r)
log_2 := or(log_2, shl(56, f))
r := shr(f, r)
}
assembly {
r := shr(127, mul(r, r))
let f := shr(128, r)
log_2 := or(log_2, shl(55, f))
r := shr(f, r)
}
assembly {
r := shr(127, mul(r, r))
let f := shr(128, r)
log_2 := or(log_2, shl(54, f))
r := shr(f, r)
}
assembly {
r := shr(127, mul(r, r))
let f := shr(128, r)
log_2 := or(log_2, shl(53, f))
r := shr(f, r)
}
assembly {
r := shr(127, mul(r, r))
let f := shr(128, r)
log_2 := or(log_2, shl(52, f))
r := shr(f, r)
}
assembly {
r := shr(127, mul(r, r))
let f := shr(128, r)
log_2 := or(log_2, shl(51, f))
r := shr(f, r)
}
assembly {
r := shr(127, mul(r, r))
let f := shr(128, r)
log_2 := or(log_2, shl(50, f))
}
int256 log_sqrt10001 = log_2 * 255738958999603826347141; // 128.128 number
int24 tickLow = int24((log_sqrt10001 - 3402992956809132418596140100660247210) >> 128);
int24 tickHi = int24((log_sqrt10001 + 291339464771989622907027621153398088495) >> 128);
tick = tickLow == tickHi ? tickLow : getSqrtRatioAtTick(tickHi) <= sqrtPriceX96 ? tickHi : tickLow;
}
这个函数的实现思路其实是一样的,但是它根据 Uniswap v3 项目中的需求,进行了一些改造和计算复杂度的优化。我们还是拆解来看:
uint256 ratio = uint256(sqrtPriceX96) << 32;
首先将输入转换成 Q128.128 定点数。接下来还是要求 MSB 的位数:
uint256 r = ratio;
uint256 msb = 0;
assembly {
let f := shl(7, gt(r, 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF)) // if (r >= 2^128) f = 128(即 1<<7)
msb := or(msb, f) // msb += f
r := shr(f, r) // r >>= 128
}
assembly {
let f := shl(6, gt(r, 0xFFFFFFFFFFFFFFFF))
msb := or(msb, f)
r := shr(f, r)
}
// 省略中间相似代码
assembly {
let f := shl(1, gt(r, 0x3))
msb := or(msb, f)
r := shr(f, r)
}
assembly {
let f := gt(r, 0x1)
msb := or(msb, f)
}
这里使用了 Yul 汇编码实现,其本质还是通过二分查找的方式计算出 MSB 的位数值。奇怪的是,Uniswap v3 代码中还用 solidity 重新实现了一遍这个过程,见:BitMath.sol.
注意,上面计算出的 msb 也是一个 Q128.128 定点数,接下来的代码:
if (msb >= 128) r = ratio >> (msb - 127);
else r = ratio << (127 - msb);
我们先只考虑当 msb >= 128 时,即 r >= 1 时。这里右移 msb 位就是计算就是之前公式中的计算 $\frac{r}{2^{n}}$. 因为 r 是 Q128.128 定点数,msb 是 r 的 MSB 位数,那么 r 整数部分的位数即为 n = msb - 128,那么上面的式子可以转换成(为了便于理解,这里不考虑溢出问题):
if (msb >= 128) r = ratio >> 128 >> n << 127;
最后得到的 r 即为一个 Q129.127 定点数,其值为 $\frac{r}{2^{n}}$. 计算出这个值之后就可以准备开始迭代计算 log_2 结果的小数部分了。
int256 log_2 = (int256(msb) - 128) << 64;
在计算小数部分之前,先把整数部分的结果记录下来,这里使用 Q64 64位定点数。
关于小数部分的计算,由于这个函数最终要返回的结果的 tick index 是一个整数,这里在计算 $log_2x$ 时可以不需要那么的精确,只需要将最后计算结果的误差保持在 ±1 之内就可以。
迭代计算小数部分:
assembly {
r := shr(127, mul(r, r)) // 先计算 r := r^2,然后右移 127 位使其成为 Q129.127 定点数
let f := shr(128, r) // 右移 128 位,那么现在的第 0 位即为上一步操作结果中,整数位第 1 位的值,和 ABDK 同理,当其 f 为 1 时 r >= 2
log_2 := or(log_2, shl(63, f)) // 如果 r >= 2,进行与操作(即加法操作),这里使用 f 左移 63 位,当 f 为 1 时,这里等价于 log_2 += 1/2
r := shr(f, r) // 如果 r >= 2,r := r / 2
}
assembly {
r := shr(127, mul(r, r)) // 重复进行上面的操作,这里计算的是小数点后第二位,即第 63 位(1<<62),即 if (r^2 >= 2) log2 += 1/4, r := r/2
let f := shr(128, r)
log_2 := or(log_2, shl(62, f))
r := shr(f, r)
}
// ...省略中间相似代码
assembly {
r := shr(127, mul(r, r)) // 一直计算至第 51 位,即二进制小数点后 14 位
let f := shr(128, r)
log_2 := or(log_2, shl(50, f))
}
这里仍然使用了 Yul 汇编码,其实现和 ABDK 仍然相同,但是 Uniswap 去掉了迭代循环,而是使用重复的汇编码,最终计算精度至小数部分二进制表示中的第 51 位的值。
这样我们就计算出了 $log_2r$ 的近似值,接下来就可以计算出 $log_{\sqrt{1.0001}}r$ 的近似值:
int256 log_sqrt10001 = log_2 * 255738958999603826347141; // 128.128 number
这里的 magic number 255738958999603826347141 即为 $(log_{\sqrt{1.0001}}2)$«64 的值,因为 log_2 是 Q64 的定点数,继续左移 64 位之后,得到一个 Q128.128 的定点数。
int24 tickLow = int24((log_sqrt10001 - 3402992956809132418596140100660247210) >> 128);
int24 tickHi = int24((log_sqrt10001 + 291339464771989622907027621153398088495) >> 128);
tick = tickLow == tickHi ? tickLow : getSqrtRatioAtTick(tickHi) <= sqrtPriceX96 ? tickHi : tickLow;
接下来,使用对数的结果,计算出 tickLow 和 tickHi。即为此对数结果附近的两个 tick index,最后使用 tick index 反向计算出 $\sqrt{P}$ 并与输入比较验证,得出最近的 tick index,并且满足此 tick index 对应的 tick_ratio <= input_ratio.
在前面计算对数结果的时候,代码在计算 $log_2r$ 的时候只计算到了二进制小数点后第 14 位,即存在一定的误差,在后续的 int256 log_sqrt10001 = log_2 * 255738958999603826347141 这一步计算中,这个误差被进一步的放大了。所以在最后需要对结果进行一些误差补偿。
上面代码中的 3402992956809132418596140100660247210 和 291339464771989622907027621153398088495 两个 magic number 是误差补偿,但是因为没有代码注释,这里笔者只能进行一些粗略的推断(乱猜)。粗略计算得出 log2 的误差最小可能会偏小 0.8461692350358629,而 291339464771989622907027621153398088495 表示 0.8561697375276566 可以弥补这个补偿,
最终在补偿后结果上进行反向计算,并且找出最终合适的 tick index.
总的来说,Uniswap V3 中对数计算的思路也是和 ABDK 中一致,但是因为它的特殊需求,不需要在代码中一直进行迭代,只需要计算出可接受范围内精度的结果即可。同时 uniswap 中还使用 yul 汇编的 bit operation 进行了执行效率优化。
扩展阅读
关于 Solidity 对数计算的话题就结束了,Happy coding!
下面是代码阅读和本文撰写过程中参考的资料: