Uniswap v3 详解(二):创建交易对/提供流动性
前文已经说过 Uniswap v3 的代码架构。一般来说,用户的操作都是从 uniswap-v3-periphery 中的合约开始。
创建交易对
创建交易对的调用流程如下:
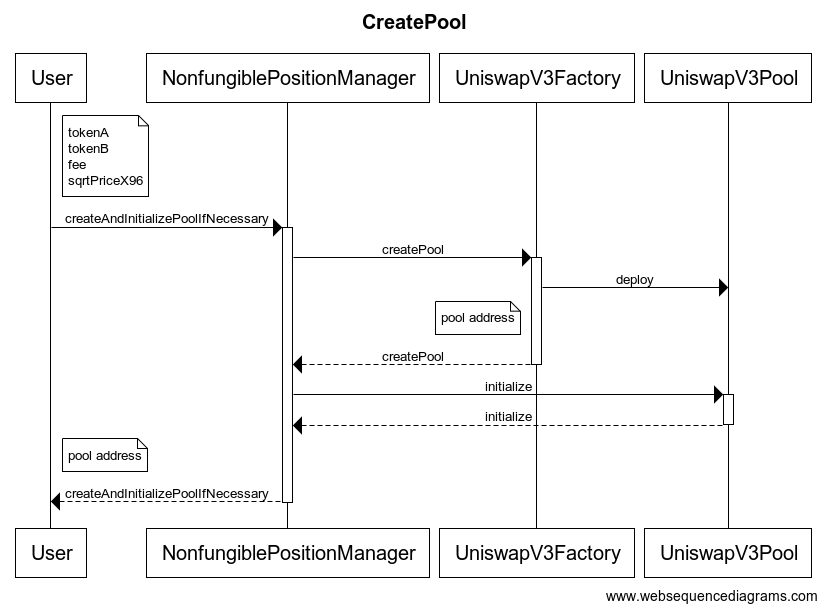
用户首先调用 NonfungiblePositionManager 合约的 createAndInitializePoolIfNecessary 方法创建交易对,传入的参数为交易对的 token0, token1, fee 和初始价格 $\sqrt P$.
NonfungiblePositionManager 合约内部通过调用 UniswapV3Factory 的 createPool 方法完成交易对的创建,然后对交易对进行初始化,初始化的作用就是给交易对设置一个初始的价格。
createAndInitializePoolIfNecessary 如下:
function createAndInitializePoolIfNecessary(
address tokenA,
address tokenB,
uint24 fee,
uint160 sqrtPriceX96
) external payable returns (address pool) {
pool = IUniswapV3Factory(factory).getPool(tokenA, tokenB, fee);
if (pool == address(0)) {
pool = IUniswapV3Factory(factory).createPool(tokenA, tokenB, fee);
IUniswapV3Pool(pool).initialize(sqrtPriceX96);
} else {
(uint160 sqrtPriceX96Existing, , , , , , ) = IUniswapV3Pool(pool).slot0();
if (sqrtPriceX96Existing == 0) {
IUniswapV3Pool(pool).initialize(sqrtPriceX96);
}
}
}
首先调用 UniswapV3Factory.getPool 方法查看交易对是否已经创建,getPool 函数是 solidity 自动为 UniswapV3Factory 合约中的状态变量 getPool 生成的外部函数,getPool 的数据类型为:
contract UniswapV3Factory is IUniswapV3Factory, UniswapV3PoolDeployer, NoDelegateCall {
...
mapping(address => mapping(address => mapping(uint24 => address))) public override getPool;
...
}
使用 3个 map 说明了 v3 版本使用 (tokenA, tokenB, fee) 来作为一个交易对的键,即相同代币,不同费率之间的流动池不一样。另外对于给定的 tokenA 和 tokenB,会先将其地址排序,将地址值更小的放在前,这样方便后续交易池的查询和计算。
再来看 UniswapV3Factory 创建交易对的过程,实际上它是调用 deploy 函数完成交易对的创建:
function deploy(
address factory,
address token0,
address token1,
uint24 fee,
int24 tickSpacing
) internal returns (address pool) {
parameters = Parameters({factory: factory, token0: token0, token1: token1, fee: fee, tickSpacing: tickSpacing});
pool = address(new UniswapV3Pool{salt: keccak256(abi.encode(token0, token1, fee))}());
delete parameters;
}
这里的 fee 和 tickSpacing 是和费率及价格最小间隔相关的设置,这里只关注创建过程,费率和 tick 的实现后面再来做介绍。
CREATE2
创建交易对,就是创建一个新的合约,作为流动池来提供交易功能。创建合约的步骤是:
pool = address(new UniswapV3Pool{salt: keccak256(abi.encode(token0, token1, fee))}());
这里先通过 keccak256(abi.encode(token0, token1, fee) 将 token0, token1, fee 作为输入,得到一个哈希值,并将其作为 salt 来创建合约。因为指定了 salt, solidity 会使用 EVM 的 CREATE2 指令来创建合约。使用 CREATE2 指令的好处是,只要合约的 bytecode 及 salt 不变,那么创建出来的地址也将不变。
关于使用 salt 创建合约的解释:Salted contract creations / create2
CREATE2指令的具体解释可以参考:EIP-1014。solidity 在 0.6.2 版本后在语法层面支持了CREATE2. 如果使用更低的版本,可以参考 Uniswap v2 的代码实现同样的功能。
使用 CREATE2 的好处是:
- 可以在链下计算出已经创建的交易池的地址
- 其他合约不必通过
UniswapV3Factory中的接口来查询交易池的地址,可以节省 gas - 合约地址不会因为 reorg 而改变
不需要通过 UniswapV3Factory 的接口来计算交易池合约地址的方法,可以看这段代码。
新交易对合约的构造函数中会反向查询 UniswapV3Factory 中的 parameters 值来进行初始变量的赋值:
constructor() {
int24 _tickSpacing;
(factory, token0, token1, fee, _tickSpacing) = IUniswapV3PoolDeployer(msg.sender).parameters();
tickSpacing = _tickSpacing;
maxLiquidityPerTick = Tick.tickSpacingToMaxLiquidityPerTick(_tickSpacing);
}
为什么不直接使用参数传递来对新合约的状态变量赋值呢。这是因为 CREATE2 会将合约的 initcode 和 salt 一起用来计算创建出的合约地址。而 initcode 是包含 contructor code 和其参数的,如果合约的 constructor 函数包含了参数,那么其 initcode 将因为其传入参数不同而不同。在 off-chain 计算合约地址时,也需要通过这些参数来查询对应的 initcode。为了让合约地址的计算更简单,这里的 constructor 不包含参数(这样合约的 initcode 将时唯一的),而是使用动态 call 的方式来获取其创建参数。
最后,对创建的交易对合约进行初始化:
function initialize(uint160 sqrtPriceX96) external override {
require(slot0.sqrtPriceX96 == 0, 'AI');
int24 tick = TickMath.getTickAtSqrtRatio(sqrtPriceX96);
(uint16 cardinality, uint16 cardinalityNext) = observations.initialize(_blockTimestamp());
slot0 = Slot0({
sqrtPriceX96: sqrtPriceX96,
tick: tick,
observationIndex: 0,
observationCardinality: cardinality,
observationCardinalityNext: cardinalityNext,
feeProtocol: 0,
unlocked: true
});
emit Initialize(sqrtPriceX96, tick);
}
初始化主要是设置了交易池的初始价格(注意,此时池子中还没有流动性),以及费率,tick 等相关变量的初始化。完成之后一个交易池就创建好了。
提供流动性
在合约内,v3 会保存所有用户的流动性,代码内称作 Position,提供流动性的调用流程如下:
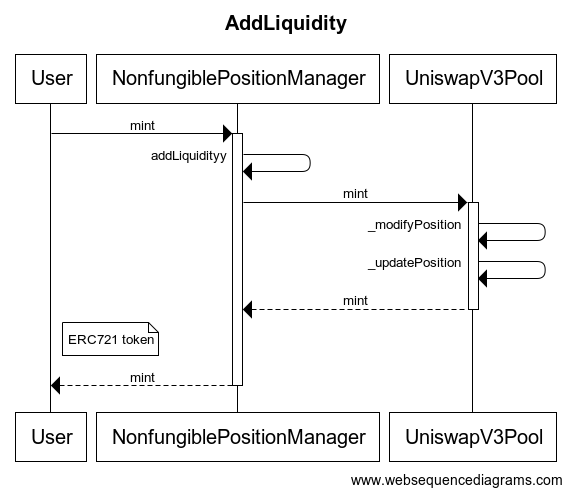
用户还是首先和 NonfungiblePositionManager 合约交互。v3 这次将 LP token 改成了 ERC721 token,并且将 token 功能放到 NonfungiblePositionManager 合约中。这个合约替代用户完成提供流动性操作,然后根据将流动性的数据元记录下来,并给用户铸造一个 NFT Token.
省略部分非关键步骤,我们先来看添加流动性的函数:
struct AddLiquidityParams {
address token0; // token0 的地址
address token1; // token1 的地址
uint24 fee; // 交易费率
address recipient; // 流动性的所属人地址
int24 tickLower; // 流动性的价格下限(以 token0 计价),这里传入的是 tick index
int24 tickUpper; // 流动性的价格上线(以 token0 计价),这里传入的是 tick index
uint128 amount; // 流动性 L 的值
uint256 amount0Max; // 提供的 token0 上限数
uint256 amount1Max; // 提供的 token1 上限数
}
function addLiquidity(AddLiquidityParams memory params)
internal
returns (
uint256 amount0,
uint256 amount1,
IUniswapV3Pool pool
)
{
PoolAddress.PoolKey memory poolKey =
PoolAddress.PoolKey({token0: params.token0, token1: params.token1, fee: params.fee});
// 这里不需要访问 factory 合约,可以通过 token0, token1, fee 三个参数计算出 pool 的合约地址
pool = IUniswapV3Pool(PoolAddress.computeAddress(factory, poolKey));
(amount0, amount1) = pool.mint(
params.recipient,
params.tickLower,
params.tickUpper,
params.amount,
// 这里是 pool 合约回调所使用的参数
abi.encode(MintCallbackData({poolKey: poolKey, payer: msg.sender}))
);
require(amount0 <= params.amount0Max);
require(amount1 <= params.amount1Max);
}
这里有几点值得注意:
传入的 lower/upper 价格是以 tick index 来表示的,因此需要在链下先计算好价格所对应的 tick index
传入的是流动性 $L$ 的大小,这个也需要在链下先计算好,计算过程见下面
我们不需要访问 factory 就可以计算出 pool 的地址,实现原理见 CREATE2
这里有一个回调函数的参数。v3 使用回调函数来完成进行流动性 token 的支付操作,原因见下面
从 token 数计算流动性 L
如前所述,因为合约的参数接受的是流动性 $L$ 的值,我们需要在链下通过用户愿意提供流动性包含的 token 数,计算出 $L$,这部分计算需要在前端界面预先算好, (2020.06.06 更新,在 uniswap 最新的代码中,简化了接口的参数,不在需要在链下预计算 L,这部分计算已经在合约中实现了,但是原理是不变的,为了保持本文的完整性,文本不再进行修改,关于 uniswap 合约和本文中代码的差异,可以在看完本文后看这个 commit)。
假设用户提供流动性的价格范围是:$[P_a, \ P_b]\ (P_a < P_b)$,代币池中的当前价格为 $P_c$,可以分成三种情况来计算流动性 $L$ 的值:
- 当前池中的价格 $P_{c} < P_{a}$ ,如下图:
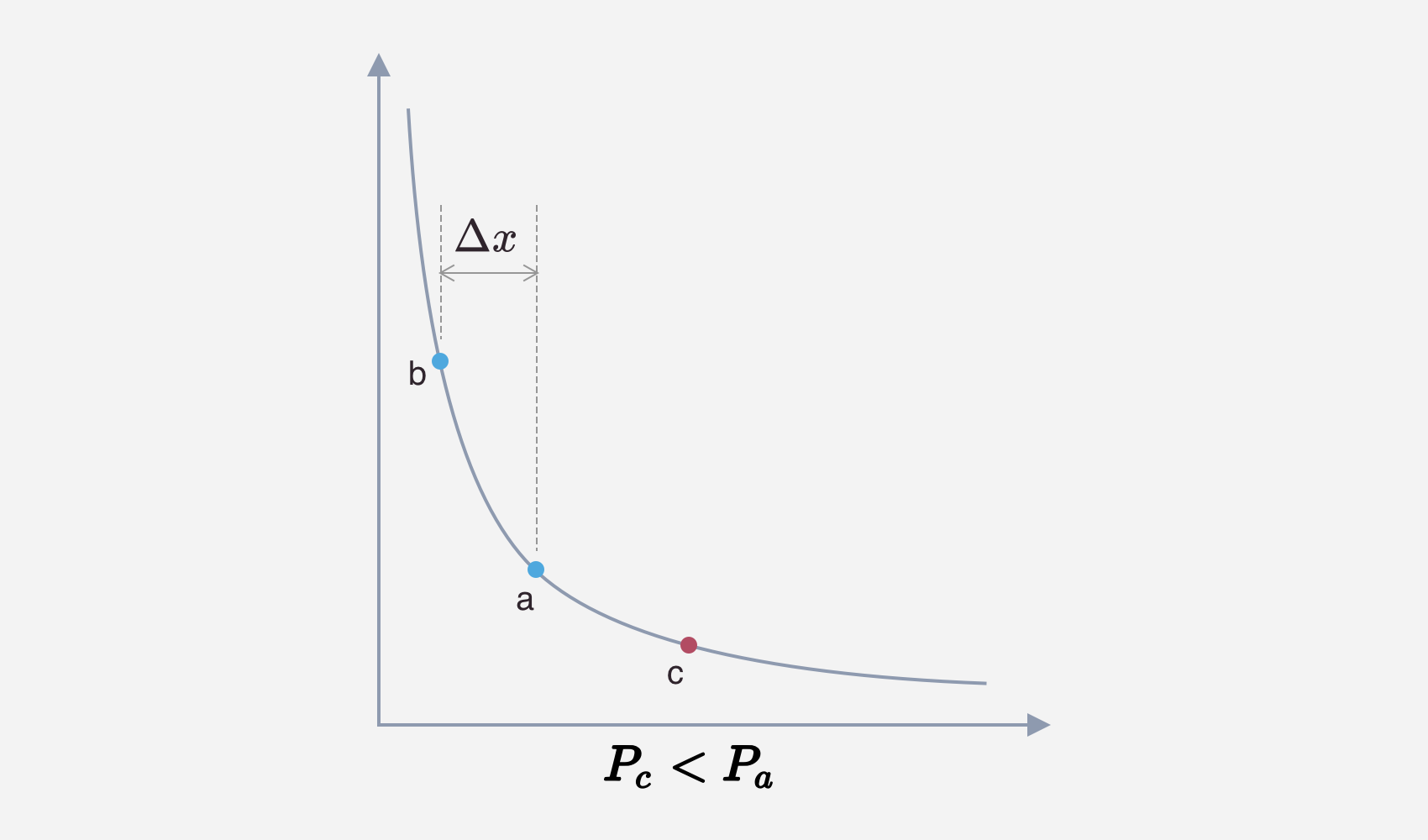
此时添加的流动性全部为 x token,计算 $L$:
$$ L = \frac {\Delta x}{\frac 1{\sqrt {P_{a}}} - \frac 1{\sqrt {P_{b}}}} $$
- 当前池中的价格 $P_{c} > P_{b}$
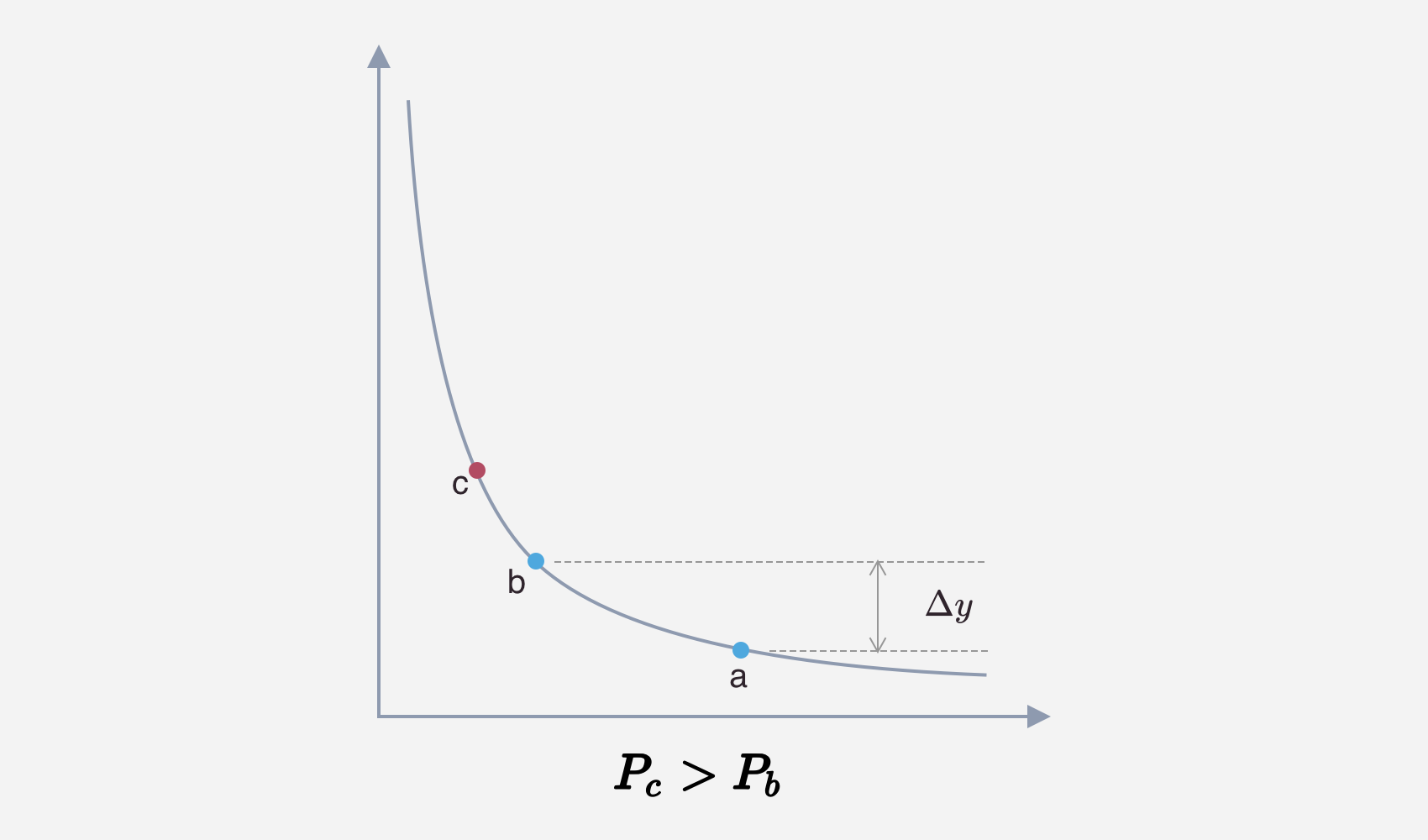
此时添加的流动性全部为 y token,计算 $L$:
$$ L = \frac {\Delta y}{\sqrt {P_{b}} - \sqrt {P_{a}}} $$
- 当前池子中的价格 $P_{c} \in [P_{a}, P_{b}]$,如下图:
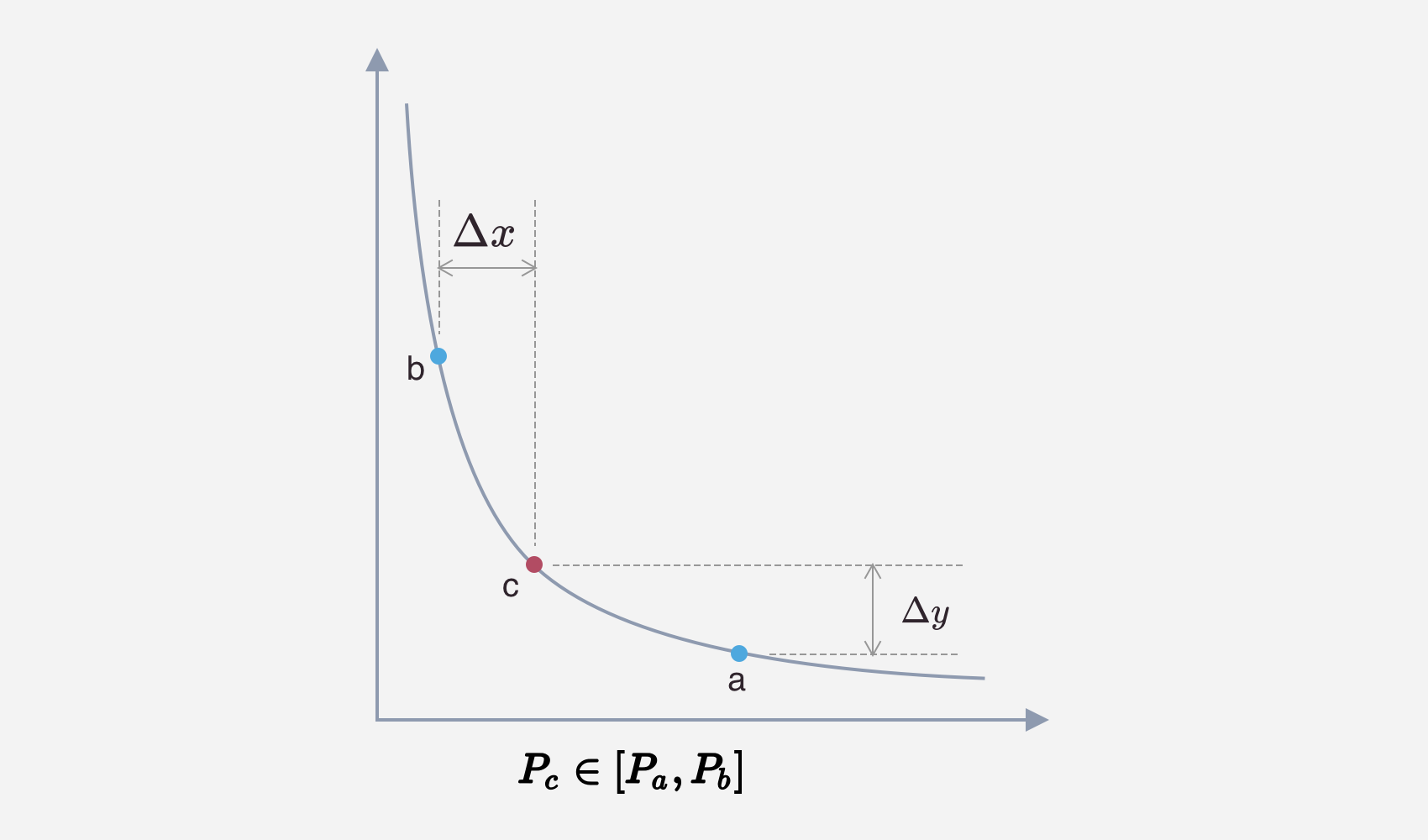
此时添加的流动性包含两个币种,可以通过任意一个 token 数量计算出 $L$:
$$ L = \frac {\Delta x}{\frac 1{\sqrt {P_{c}}} - \frac 1{\sqrt {P_{b}}}} = \frac {\Delta y}{\sqrt {P_{c}} - \sqrt {P_{a}}} $$
回调函数
使用回调函数原因是,将 Position 的 owner 和实际流动性 token 支付者解耦。这样可以让中间合约来管理用户的流动性,并将流动性 token 化。关于 token 化,Uniswap v3 默认实现了 ERC721 token(因为即使是同一个池子,流动性之间差异也也很大)。
例如,当用户通过 NonfungiblePositionManager 来提供流动性时,对于 UniswapV3Pool 合约来说,这个 Position 的 owner 是 NonfungiblePositionManager,而 NonfungiblePositionManager 再通过 NFT Token 将 Position 与用户关联起来。这样用户就可以将 LP token 进行转账或者抵押类操作。
在 NonfungiblePositionManager 中回调函数的实现如下:
struct MintCallbackData {
PoolAddress.PoolKey poolKey;
address payer; // 支付 token 的地址
}
/// @inheritdoc IUniswapV3MintCallback
function uniswapV3MintCallback(
uint256 amount0Owed,
uint256 amount1Owed,
bytes calldata data
) external override {
MintCallbackData memory decoded = abi.decode(data, (MintCallbackData));
CallbackValidation.verifyCallback(factory, decoded.poolKey);
// 根据传入的参数,使用 transferFrom 代用户向 Pool 中支付 token
if (amount0Owed > 0) pay(decoded.poolKey.token0, decoded.payer, msg.sender, amount0Owed);
if (amount1Owed > 0) pay(decoded.poolKey.token1, decoded.payer, msg.sender, amount1Owed);
}
postion 更新
接着我们看 UniswapV3Pool 是如何添加流动性的。流动性的添加主要在 UniswapV3Pool._modifyPosition 中,这个函会先调用 _updatePosition 来创建或修改一个用户的 Position,省略其中的非关键步骤:
function _updatePosition(
address owner,
int24 tickLower,
int24 tickUpper,
int128 liquidityDelta,
int24 tick
) private returns (Position.Info storage position) {
// 获取用户的 Postion
position = positions.get(owner, tickLower, tickUpper);
...
// 根据传入的参数修改 Position 对应的 lower/upper tick 中
// 的数据,这里可以是增加流动性,也可以是移出流动性
bool flippedLower;
bool flippedUpper;
if (liquidityDelta != 0) {
uint32 blockTimestamp = _blockTimestamp();
// 更新 lower tikc 和 upper tick
// fippedX 变量表示是此 tick 的引用状态是否发生变化,即
// 被引用 -> 未被引用 或
// 未被引用 -> 被引用
// 后续需要根据这个变量的值来更新 tick 位图
flippedLower = ticks.update(
tickLower,
tick,
liquidityDelta,
_feeGrowthGlobal0X128,
_feeGrowthGlobal1X128,
false,
maxLiquidityPerTick
);
flippedUpper = ticks.update(
tickUpper,
tick,
liquidityDelta,
_feeGrowthGlobal0X128,
_feeGrowthGlobal1X128,
true,
maxLiquidityPerTick
);
// 如果一个 tick 第一次被引用,或者移除了所有引用
// 那么更新 tick 位图
if (flippedLower) {
tickBitmap.flipTick(tickLower, tickSpacing);
secondsOutside.initialize(tickLower, tick, tickSpacing, blockTimestamp);
}
if (flippedUpper) {
tickBitmap.flipTick(tickUpper, tickSpacing);
secondsOutside.initialize(tickUpper, tick, tickSpacing, blockTimestamp);
}
}
...
// 更新 position 中的数据
position.update(liquidityDelta, feeGrowthInside0X128, feeGrowthInside1X128);
// 如果移除了对 tick 的引用,那么清除之前记录的元数据
// 这只会发生在移除流动性的操作中
if (liquidityDelta < 0) {
if (flippedLower) {
ticks.clear(tickLower);
secondsOutside.clear(tickLower, tickSpacing);
}
if (flippedUpper) {
ticks.clear(tickUpper);
secondsOutside.clear(tickUpper, tickSpacing);
}
}
}
先忽略费率相关的操作,这个函数所做的操作是:
- 添加/移除流动性时,先更新这个 Positon 对应的 lower/upper tick 中记录的元数据
- 更新 position
- 根据需要更新 tick 位图
Postion 是以 owner, lower tick, uppper tick 作为键来存储的,注意这里的 owner 实际上是 NonfungiblePositionManager 合约的地址。这样当多个用户在同一个价格区间提供流动性时,在底层的 UniswapV3Pool 合约中会将他们合并存储。而在 NonfungiblePositionManager 合约中会按用户来区别每个用户拥有的 Position.
Postion 中包含的字段中,除去费率相关的字段,只有一个即流动性 $L$:
library Position {
// info stored for each user's position
struct Info {
// 此 position 中包含的流动性大小,即 L 值
uint128 liquidity;
...
}
更新 position 只需要一行调用:
position.update(liquidityDelta, feeGrowthInside0X128, feeGrowthInside1X128);
其中包含了 position 中流动性 $L$ 的更新,以及手续费相关的计算。
tick 管理
我们再来看 tick 相关的管理,在 UniswapV3Pool 合约中有两个状态变量记录了 tick 相关的信息:
// tick 元数据管理的库
using Tick for mapping(int24 => Tick.Info);
// tick 位图槽位的库
using TickBitmap for mapping(int16 => uint256);
// 记录了一个 tick 包含的元数据,这里只会包含所有 Position 的 lower/upper ticks
mapping(int24 => Tick.Info) public override ticks;
// tick 位图,因为这个位图比较长(一共有 887272x2 个位),大部分的位不需要初始化
// 因此分成两级来管理,每 256 位为一个单位,一个单位称为一个 word
// map 中的键是 word 的索引
mapping(int16 => uint256) public override tickBitmap;
library Tick {
...
// tick 中记录的数据
struct Info {
// 记录了所有引用这个 tick 的 position 流动性的和
uint128 liquidityGross;
// 当此 tick 被越过时(从左至右),池子中整体流动性需要变化的值
int128 liquidityNet;
...
}
tick 中和流动性相关的字段有两个 liquidityGross,liquidityNet。
liquidityNet 表示当价格从左至右经过此 tick 时整体流动性需要变化的净值。在单个流动性中,对于 lower tick 来说,它的值为正,对于 upper tick 来说它的值为 负。
如果有两个 position 中的流动性相等,例如 L = 500,并且这两个 position 同时引用了一个 tick,其中一个为 lower tick ,另一个为 upper tick,那么对于这个 tick,它的 liquidityNet = 0。此时我们就需要有一种机制来判断一个 tick 是否仍然在被引用中。这里使用 liquidityGross 记录流动性的增值(不考虑 lower/upper),我们可以就通过流动性变化前后 liquidityGross 是否等于 0 来判断这个 tick 是否仍被引用。
当价格变动导致 $tick_{current}$ 越过一个 position 的 lower/upper tick 时,我们需要根据 tick 中记录的值来更新当前价格所对应的总体流动性。假设 position 的流动性值为 $\Delta L$,会有以下四种情况:
- token0 价格上升,即从左至右越过一个 lower tick 时, $L=L_{current} + \Delta L$
- token0 价格上升,即从左至右越过一个 upper tick 时, $L=L_{current} - \Delta L$
- token0 价格下降,即从右至左越过一个 upper tick 时, $L=L_{current} + \Delta L$
- token0 价格下降,即从右至左越过一个 lower tick 时, $L=L_{current} - \Delta L$
liquidityNet 中记录的就是当从左至右穿过这个 tick 时,需要增减的流动性,当其为 lower tick 时,其值为正,当其为 upper tick 时,其值为负。对于从右至左穿过的情况,只需将 liquidityNet 的值去翻即可完成计算。
我再来看如何更新 tick 元数据,以下是 tick.update 函数:
function update(
mapping(int24 => Tick.Info) storage self,
int24 tick,
int24 tickCurrent,
int128 liquidityDelta,
uint256 feeGrowthGlobal0X128,
uint256 feeGrowthGlobal1X128,
bool upper,
uint128 maxLiquidity
) internal returns (bool flipped) {
Tick.Info storage info = self[tick];
uint128 liquidityGrossBefore = info.liquidityGross;
uint128 liquidityGrossAfter = LiquidityMath.addDelta(liquidityGrossBefore, liquidityDelta);
require(liquidityGrossAfter <= maxLiquidity, 'LO');
// 通过 liquidityGross 在进行 position 变化前后的值
// 来判断 tick 是否仍被引用
flipped = (liquidityGrossAfter == 0) != (liquidityGrossBefore == 0);
...
info.liquidityGross = liquidityGrossAfter;
// 更新 liquidityNet 的值,对于 upper tick,
info.liquidityNet = upper
? int256(info.liquidityNet).sub(liquidityDelta).toInt128()
: int256(info.liquidityNet).add(liquidityDelta).toInt128();
}
此函数返回的 flipped 表示此 tick 的引用状态是否发生变化,之前的 _updatePosition 中的代码会根据这个返回值去更新 tick 位图。
tick 位图
tick 位图用于记录所有被引用的 lower/upper tick index,我们可以用过 tick 位图,从当前价格找到下一个(从左至右或者从右至左)被引用的 tick index。关于 tick 位图的管理,在 _updatePosition 中的:
if (flippedLower) {
tickBitmap.flipTick(tickLower, tickSpacing);
secondsOutside.initialize(tickLower, tick, tickSpacing, blockTimestamp);
}
if (flippedUpper) {
tickBitmap.flipTick(tickUpper, tickSpacing);
secondsOutside.initialize(tickUpper, tick, tickSpacing, blockTimestamp);
}
这里不做进一步的说明,具体代码实现在TickBitmap库中。tick 位图有以下几个特性:
- 对于不存在的 tick,不需要初始值,因为访问 map 中不存在的 key 默认值就是 0
- 通过对位图的每个 word(uint256) 建立索引来管理位图,即访问路径为 word index -> word -> tick bit
token 数确认
_modifyPosition 函数在调用 _updatePosition 更新完 Position 后,会计算出此次提供流动性具体所需的 x token 和 y token 数量。
function _modifyPosition(ModifyPositionParams memory params)
private
noDelegateCall
returns (
Position.Info storage position,
int256 amount0,
int256 amount1
)
{
...
Slot0 memory _slot0 = slot0; // SLOAD for gas optimization
position = _updatePosition(
...
);
...
}
这里插入一个题外话,这一行代码:
Slot0 memory _slot0 = slot0; // SLOAD for gas optimization
因为后续需要多次访问 slot0,这里将其读入内存中,后续的访问就可以使用 MLOAD 而不用使用 SLOAD,可以节省 gas(SLOAD 的成本比 MLOAD 高很多)。Uniswap v2 和 v3 大量使用了这个技巧。
这个函数在更新完 position 之后,主要做的就是通过 $L$ 和 $\Delta \sqrt P$ 计算出用户需要支付的 token 数量,我们之前已经讲过 从 token 数计算流动性 L的三种情况,这里其实就是之前计算的逆运算,即通过 $L$ 计算 x token 和 y token 的数量,这里不再重复赘述其公式。具体代码如下:
function _modifyPosition(ModifyPositionParams memory params)
private
noDelegateCall
returns (
Position.Info storage position,
int256 amount0,
int256 amount1
)
{
...
if (params.liquidityDelta != 0) {
// 计算三种情况下 amount0 和 amount1 的值,即 x token 和 y token 的数量
if (_slot0.tick < params.tickLower) {
amount0 = SqrtPriceMath.getAmount0Delta(
// 计算 lower/upper tick 对应的价格
TickMath.getSqrtRatioAtTick(params.tickLower),
TickMath.getSqrtRatioAtTick(params.tickUpper),
params.liquidityDelta
);
} else if (_slot0.tick < params.tickUpper) {
// current tick is inside the passed range
uint128 liquidityBefore = liquidity; // SLOAD for gas optimization
...
amount0 = SqrtPriceMath.getAmount0Delta(
_slot0.sqrtPriceX96,
TickMath.getSqrtRatioAtTick(params.tickUpper),
params.liquidityDelta
);
amount1 = SqrtPriceMath.getAmount1Delta(
TickMath.getSqrtRatioAtTick(params.tickLower),
_slot0.sqrtPriceX96,
params.liquidityDelta
);
liquidity = LiquidityMath.addDelta(liquidityBefore, params.liquidityDelta);
} else {
amount1 = SqrtPriceMath.getAmount1Delta(
TickMath.getSqrtRatioAtTick(params.tickLower),
TickMath.getSqrtRatioAtTick(params.tickUpper),
params.liquidityDelta
);
}
}
}
代码将计算的过程封装在了 SqrtPriceMath 库中,getAmount0Delta 和 getAmount1Delta 分别对应公式 $\Delta x = \Delta {\frac 1{\sqrt P}} \cdot L$ 和 $\Delta y = \Delta \sqrt P \cdot L$.
在具体的计算过程中,又分成了 RoundUp 和 RoundDown 两种情况,简单来说:
- 当提供/增加流动性时,会使用 RoundUp,这样可以保证增加数量为 L 的流动性时,用户提供足够的 token 到 pool 中
- 当移除/减少流动性时,会使用 RoundDown,这样可以保证减少数量为 L 的流动性时,不会从 pool 中给用户多余的 token
通过上述两个条件可以保证 pool 在流动性增加/移除的操作中,不会出现坏账的情况。除了流动性操作之外,swap 操作也会使用类似机制,保证 pool 不会出现坏账。
同时,Uniswap v3 参考这里实现了一个精度较高的 $\frac {a \cdot b}c$ 的算法,封装在 FullMath 库中。
tick index -> $\sqrt P$
上面的代码还使用了 TickMath 库中的 getSqrtRatioAtTick 来通过 tick index 计算其所对应的价格,实现为:
function getSqrtRatioAtTick(int24 tick) internal pure returns (uint160 sqrtPriceX96) {
uint256 absTick = tick < 0 ? uint256(-int256(tick)) : uint256(int256(tick));
require(absTick <= uint256(MAX_TICK), 'T');
// 这些魔数分别表示 1/sqrt(1.0001)^1, 1/sqrt(1.0001)^2, 1/sqrt(1.0001)^4....
uint256 ratio = absTick & 0x1 != 0 ? 0xfffcb933bd6fad37aa2d162d1a594001 : 0x100000000000000000000000000000000;
if (absTick & 0x2 != 0) ratio = (ratio * 0xfff97272373d413259a46990580e213a) >> 128;
if (absTick & 0x4 != 0) ratio = (ratio * 0xfff2e50f5f656932ef12357cf3c7fdcc) >> 128;
if (absTick & 0x8 != 0) ratio = (ratio * 0xffe5caca7e10e4e61c3624eaa0941cd0) >> 128;
if (absTick & 0x10 != 0) ratio = (ratio * 0xffcb9843d60f6159c9db58835c926644) >> 128;
if (absTick & 0x20 != 0) ratio = (ratio * 0xff973b41fa98c081472e6896dfb254c0) >> 128;
if (absTick & 0x40 != 0) ratio = (ratio * 0xff2ea16466c96a3843ec78b326b52861) >> 128;
if (absTick & 0x80 != 0) ratio = (ratio * 0xfe5dee046a99a2a811c461f1969c3053) >> 128;
if (absTick & 0x100 != 0) ratio = (ratio * 0xfcbe86c7900a88aedcffc83b479aa3a4) >> 128;
if (absTick & 0x200 != 0) ratio = (ratio * 0xf987a7253ac413176f2b074cf7815e54) >> 128;
if (absTick & 0x400 != 0) ratio = (ratio * 0xf3392b0822b70005940c7a398e4b70f3) >> 128;
if (absTick & 0x800 != 0) ratio = (ratio * 0xe7159475a2c29b7443b29c7fa6e889d9) >> 128;
if (absTick & 0x1000 != 0) ratio = (ratio * 0xd097f3bdfd2022b8845ad8f792aa5825) >> 128;
if (absTick & 0x2000 != 0) ratio = (ratio * 0xa9f746462d870fdf8a65dc1f90e061e5) >> 128;
if (absTick & 0x4000 != 0) ratio = (ratio * 0x70d869a156d2a1b890bb3df62baf32f7) >> 128;
if (absTick & 0x8000 != 0) ratio = (ratio * 0x31be135f97d08fd981231505542fcfa6) >> 128;
if (absTick & 0x10000 != 0) ratio = (ratio * 0x9aa508b5b7a84e1c677de54f3e99bc9) >> 128;
if (absTick & 0x20000 != 0) ratio = (ratio * 0x5d6af8dedb81196699c329225ee604) >> 128;
if (absTick & 0x40000 != 0) ratio = (ratio * 0x2216e584f5fa1ea926041bedfe98) >> 128;
if (absTick & 0x80000 != 0) ratio = (ratio * 0x48a170391f7dc42444e8fa2) >> 128;
if (tick > 0) ratio = type(uint256).max / ratio;
// this divides by 1<<32 rounding up to go from a Q128.128 to a Q128.96.
// we then downcast because we know the result always fits within 160 bits due to our tick input constraint
// we round up in the division so getTickAtSqrtRatio of the output price is always consistent
sqrtPriceX96 = uint160((ratio >> 32) + (ratio % (1 << 32) == 0 ? 0 : 1));
}
这段代码的实现通过很多的 magic number,优化了计算过程,其实现思路如下:
首先我们知道:
$$ \sqrt P_i = {\sqrt {1.0001}}^i $$
可以将 $i$ 拆解成如下形式,其中 $n_j$ 表示 $i$ 的二进制格式中第 $j$ 位的值:
$$ \begin{cases} i = n_0 \cdot 1 + n_1 \cdot 2 + n_2 \cdot 4 + n_3 \cdot 8 + .... \\ n_i \in \{0, 1\} \end{cases} $$例如 $i = 20 = 4 + 16$
然后我们可以有:
$$ \begin{cases} \sqrt P = {\sqrt {1.0001}}^i = {\sqrt {1.0001}}^{n_0 \cdot 1} \cdot {\sqrt {1.0001}}^{n_1 \cdot 2} \cdot {\sqrt {1.0001}}^{n_2 \cdot 4} \cdot {\sqrt {1.0001}}^{n_3 \cdot 8} \cdot ... \\ n_i \in \{0, 1\} \end{cases} $$因为 $i \in (-887272, 887272)$,只需要 20 位二进制数可以保存其值。我们可以预先算出 ${\sqrt {1.0001}}^1,\ {\sqrt {1.0001}}^2,\ {\sqrt {1.0001}}^4,\ …,\ {\sqrt {1.0001}}^{524288}$ 的值($524288=2^{19}$),然后将 $i$ 值每一位的值求出,带入上面的计算公式就可以算出 $\sqrt P_i$ 的值。
实际上,这段代码在上面的算法之上还进行了优化:
- 因为 $\sqrt {P_{-i}} = \frac 1{\sqrt P_{i}}$,所以当 $i$ 为负数时可以先将其取反,转换为正数进行计算
- 当 $i$ 的值为正数时,计算的结果可能会很大,中间计算涉及到很多乘法运算,可能会导致计算结果溢出(它使用了
Q128.128定点数)。所以实际计算的是 $i$ 为负数时的值,因为当 $i$ 为负数时,$\sqrt P_{i}$ 是一个小于 1 的小数,这样在进行乘法运算时则不会产生溢出。即上面代码的那些魔数分别为 $\frac 1{\sqrt {1.0001}^1},\ \frac 1{\sqrt {1.0001}^2},\ \frac 1{\sqrt {1.0001}^4},\ \frac 1{\sqrt {1.0001}^8},\ …,\ \frac 1{\sqrt {1.0001}^{524288}}$ 的值 - 这里的计算使用了
Q128.128精度的定点数,实际上这些魔数的值都向右移动 128 位 - 最后,当输入是正数时,我们需要在计算的结尾计算 $\sqrt P_{i} = \frac 1{\sqrt P_{-i}}$,即 $\sqrt P_{i}$ 的倒数,这里因为使用了
Q128.128精度的定点数,即计算的过程是: $\frac {1«128}{\sqrt P_{-i}} « 128 = \frac {1«256}{\sqrt P_{-i}}$,1<<256可以使用type(uint256).max取近似值来表示 - 最后的最后,将
Q128.128转换为Q64.96并始终向上取整,以保持一致性
$\sqrt P$ -> tick index
这里顺带提一下,在交易计算中会需要进行上述计算的逆计算,给定 $\sqrt P$,需要计算出对应的 tick index,即 $log_{\sqrt {1.0001}}{\sqrt P}$ 的计算。在代码中为:TickMath.getTickAtSqrtRatio,关于这个函数的实现,可以参考我的这篇文章:Solidity 中的对数计算。
完成流动性添加
_modifyPosition 调用完成后,会返回 x token, 和 y token 的数量。再来看 UniswapV3Pool.mint 的代码:
function mint(
address recipient,
int24 tickLower,
int24 tickUpper,
uint128 amount,
bytes calldata data
) external override lock returns (uint256 amount0, uint256 amount1) {
require(amount > 0);
(, int256 amount0Int, int256 amount1Int) =
_modifyPosition(
ModifyPositionParams({
owner: recipient,
tickLower: tickLower,
tickUpper: tickUpper,
liquidityDelta: int256(amount).toInt128()
})
);
amount0 = uint256(amount0Int);
amount1 = uint256(amount1Int);
uint256 balance0Before;
uint256 balance1Before;
// 获取当前池中的 x token, y token 余额
if (amount0 > 0) balance0Before = balance0();
if (amount1 > 0) balance1Before = balance1();
// 将需要的 x token 和 y token 数量传给回调函数,这里预期回调函数会将指定数量的 token 发送到合约中
IUniswapV3MintCallback(msg.sender).uniswapV3MintCallback(amount0, amount1, data);
// 回调完成后,检查发送至合约的 token 是否复合预期,如果不满足检查则回滚交易
if (amount0 > 0) require(balance0Before.add(amount0) <= balance0(), 'M0');
if (amount1 > 0) require(balance1Before.add(amount1) <= balance1(), 'M1');
emit Mint(msg.sender, recipient, tickLower, tickUpper, amount, amount0, amount1);
}
这个函数关键的步骤就是通过回调函数,让调用方发送指定数量的 x token 和 y token 至合约中。
我们再来看 NonfungiblePositionManager.mint 的代码:
function mint(MintParams calldata params)
external
payable
override
checkDeadline(params.deadline)
returns (
uint256 tokenId,
uint256 amount0,
uint256 amount1
)
{
IUniswapV3Pool pool;
// 这里是添加流动性,并完成 x token 和 y token 的发送
(amount0, amount1, pool) = addLiquidity(
AddLiquidityParams({
token0: params.token0,
token1: params.token1,
fee: params.fee,
recipient: address(this),
tickLower: params.tickLower,
tickUpper: params.tickUpper,
amount: params.amount,
amount0Max: params.amount0Max,
amount1Max: params.amount1Max
})
);
// 铸造 ERC721 token 给用户,用来代表用户所持有的流动性
_mint(params.recipient, (tokenId = _nextId++));
bytes32 positionKey = PositionKey.compute(address(this), params.tickLower, params.tickUpper);
(, uint256 feeGrowthInside0LastX128, uint256 feeGrowthInside1LastX128, , ) = pool.positions(positionKey);
// idempotent set
uint80 poolId =
cachePoolKey(
address(pool),
PoolAddress.PoolKey({token0: params.token0, token1: params.token1, fee: params.fee})
);
// 用 ERC721 的 token ID 作为键,将用户提供流动性的元信息保存起来
_positions[tokenId] = Position({
nonce: 0,
operator: address(0),
poolId: poolId,
tickLower: params.tickLower,
tickUpper: params.tickUpper,
liquidity: params.amount,
feeGrowthInside0LastX128: feeGrowthInside0LastX128,
feeGrowthInside1LastX128: feeGrowthInside1LastX128,
tokensOwed0: 0,
tokensOwed1: 0
});
}
可以看到这个函数主要是将用户的 Position 保存起来,并给用户铸造 NFT token,代表其所持有的流动性。至此提供流动性的步骤就完成了。
流动性的移除
移除流动性就是上述操作的逆操作,在 core 合约中:
function burn(
int24 tickLower,
int24 tickUpper,
uint128 amount
) external override lock returns (uint256 amount0, uint256 amount1) {
// 先计算出需要移除的 token 数
(Position.Info storage position, int256 amount0Int, int256 amount1Int) =
_modifyPosition(
ModifyPositionParams({
owner: msg.sender,
tickLower: tickLower,
tickUpper: tickUpper,
liquidityDelta: -int256(amount).toInt128()
})
);
amount0 = uint256(-amount0Int);
amount1 = uint256(-amount1Int);
// 注意这里,移除流动性后,将移出的 token 数记录到了 position.tokensOwed 上
if (amount0 > 0 || amount1 > 0) {
(position.tokensOwed0, position.tokensOwed1) = (
position.tokensOwed0 + uint128(amount0),
position.tokensOwed1 + uint128(amount1)
);
}
emit Burn(msg.sender, tickLower, tickUpper, amount, amount0, amount1);
}
移除流动性时,还是使用之前的公式计算出移出的 token 数,但是并不会直接将移出的 token 数发送给用户,而是记录在了 position 的 tokensOwed0 和 tokensOwed1 上。这样做应该是为了遵循实践:Favor pull over push for external calls.
Update 05-23
关于如何使用 ERC-721 token 来进行挖矿,可以参考这篇文章:Liquidity Mining on Uniswap v3
Uniswap v3 详解系列
本系列所有文章: