Uniswap v3 详解（三）：交易过程

Paco 收录于类别 DeFi

2021-03-28 2021-03-28 约 5713 字预计阅读 12 分钟

交易过程

v3 的 UniswapV3Pool 提供了比较底层的交易接口，而在 SwapRouter 合约中封装了面向用户的交易接口：

exactInput：指定交易对路径，付出的 x token 数和预期得到的最小 y token 数（x, y 可以互换）
exactOutput：指定交易路径，付出的 x token 最大数和预期得到的 y token 数（x, y 可以互换）

这里我们讲解 exactInput 这个接口，调用流程如下：

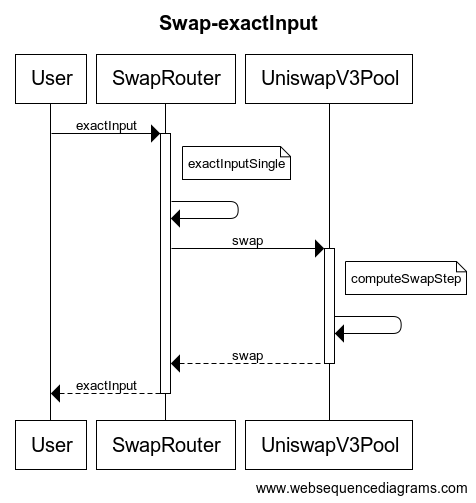
路径选择

在进行两个代币交易时，是首先需要在链下计算出交易的路径，例如使用 ETH -> DAI ：

可以直接通过 ETH/DAI 的交易池完成
也可以通过 ETH -> USDC -> DAI 路径，即经过 ETH/USDC, USDC/DAI 两个交易池完成交易

Uniswap 的前端会帮用户实时计算出最优路径（即交易的收益最高），作为参数传给合约调用。前端中这部分计算的具体实现在这里，具体过程为先用需要交易的输入代币，输出代币，以及一系列可用的中间代币（代码中叫 Base token）生成所有的路径（当然为了降低复杂度，路径中最多包含3个代币），然后遍历每个路径输出的输出代币数量，最后选取最佳路径。

事实上因为 v3 引入了费率的原因，在路径选择的过程中还需要考虑费率的因素。关于交易结果的预计算，可以参考本文末尾处更新的内容。

交易入口

交易的入口函数是 exactInput 函数，代码如下：

struct ExactInputParams {
    bytes path;                 // 路径
    address recipient;          // 收款地址
    uint256 deadline;           // 交易有效期
    uint256 amountIn;           // 输入的 token 数（输入的 token 地址就是 path 中的第一个地址）
    uint256 amountOutMinimum;   // 预期交易最少获得的 token 数（获得的 token 地址就是 path 中最后一个地址）
}

function exactInput(ExactInputParams memory params)
    external
    payable
    override
    checkDeadline(params.deadline)
    returns (uint256 amountOut)
{
    // 通过循环，遍历传入的路径，进行交易
    while (true) {
        bool hasPools = params.path.hasPools();

        // 完成当前路径的交易
        params.amountIn = exactInputSingle(
            params.amountIn,
            // 如果是中间交易，又合约代为收取和支付中间代币
            hasPools ? address(this) : params.recipient,
            // 给回调函数用的参数
            SwapData({
                path: params.path.getFirstPool(),
                payer: msg.sender
            })
        );

        // 如果路径全部遍历完成，则退出循环，交易完成
        if (hasPools) {
            // 步进 path 中的值
            params.path = params.path.skipToken();
        } else {
            amountOut = params.amountIn;
            break;
        }
    }

    // 检查交易是否满足预期
    require(amountOut >= params.amountOutMinimum, 'Too little received');
}

这里使用一个循环遍历传入的路径，路径中包含了交易过程中所有的 token，每相邻的两个 token 组成了一个交易对。例如当需要通过 ETH -> USDC -> DAI 路径进行交易时，会经过两个池：ETH/USDC 和 USDC/DAI，最终得到 DAI 代币。如前所述，这里其实还包含了每个交易对所选择的费率。

路径编码/解码

上面输入的参数中 path 字段是 bytes 类型，通过这种类型可以实现更紧凑的编码。Uniswap 会将 bytes 作为一个数组使用，bytes 类型就是一连串的 byte1，但是不会对每一个成员使用一个 word，因此相比普通数组其结构更加紧凑。在 Uniswap V3 中， path 内部编码结构如下图：

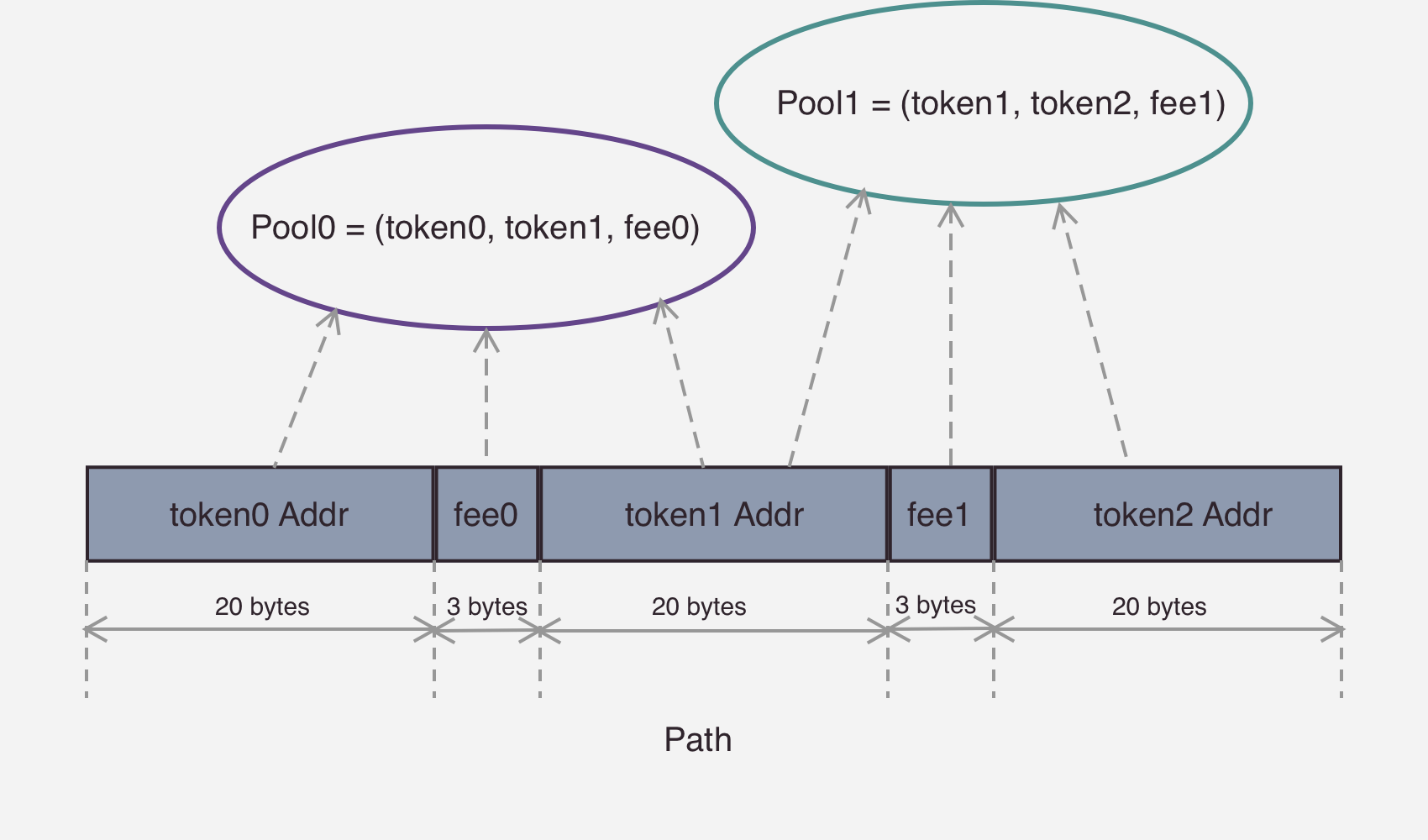
图中展示了一个包含 2个路径（pool0, 和 pool1）的 path 编码。Uniswap 将编码解码操作封装在了 Path 库中，本文不再赘述其过程。每次交易时，会取出头部的 tokenIn, tokenOut, fee，使用这三个参数找到对应的交易池，完成交易。

单个池的交易过程

单个池的交易在 exactInputSingle 函数中：

function exactInputSingle(
    uint256 amountIn,
    address recipient,
    SwapData memory data
) private returns (uint256 amountOut) {
    // 将 path 解码，获取头部的 tokenIn, tokenOut, fee
    (address tokenIn, address tokenOut, uint24 fee) = data.path.decodeFirstPool();

    // 因为交易池只保存了 token x 的价格，这里我们需要知道输入的 token 是交易池 x token 还是 y token
    bool zeroForOne = tokenIn < tokenOut;

    // 完成交易
    (int256 amount0, int256 amount1) =
        getPool(tokenIn, tokenOut, fee).swap(
            recipient,
            zeroForOne,
            amountIn.toInt256(),
            zeroForOne ? MIN_SQRT_RATIO : MAX_SQRT_RATIO,
            // 给回调函数用的参数
            abi.encode(data)
        );

    return uint256(-(zeroForOne ? amount1 : amount0));
}

交易过程就是先获取交易池，然后需要确定本次交易输入的是交易池的 x token, 还是 y token，这是因为交易池中只保存了 x 的价格 $\sqrt P = \sqrt {\frac yx}$，x token 和 y token 的计价公式是不一样的。最后调用 UniswapV3Pool 的 swap 函数完成交易。

交易分解

UniswapV3Pool.swap 函数比较长，这里先简要描述其交易步骤：

假设支付的 token 为 x

根据买入/卖出行为，$\sqrt P$ 会随着交易下降或上升，即 tick 减小或增大
在 tickBitmap 中找到和当前 tick 对应的 $i_c$ 在一个 word 中的下一个 tick 对应的 $i_n$，根据买入/卖出行为，这里分成向下查找和向上查找两种情况
如果当前 word 中没有记录其他 tick index ，那么取这个 word 的最小/最大 tick index，这么做的目的是，让单步交易中 tick 的跨度不至于太大，以减少计算中溢出的可能性（计算中会需要使用 $\Delta \sqrt P$）。
在 $[i_c, i_n]$ 价格区间内，流动性 $L$ 的值是不变的，我们可以根据 $L$ 的值计算出交易运行到 $i_n$ 时，所需要最多的 $\Delta x$ 数量
根据上一步计算的 $\Delta x$ 数量，如果满足 $\Delta x < x_{remaining}$，那么将 $i$ 设置为 $i_n$，并将 $x_remaining$ 减去需要支付的 $\Delta x$，随后跳至第 2 步继续计算（这里需要将 $i \pm tickSpace$ 使其进入位图中的下一个 word），计算之前还需要根据元数据修改当前的流动性 $L = L \pm \Delta L$
如果上一步计算 $\Delta x$，满足 $\Delta x \geq x_{remaining}$，则表示 x token 将被耗尽，则交易在此结束。
记录下结束时的价格 $\sqrt P$，将所有交易阶段的 tokenOut 数量总和返回，即为用户得到的 token 数量
上一步的计算过程还需要考虑费率的因素，为了让计算简单化，可能会多收费

我们逐步拆解 swap 函数中的代码：

...
// 将交易前的元数据保存在内存中，后续的访问通过 `MLOAD` 完成，节省 gas
Slot0 memory slot0Start = slot0;
...
// 防止交易过程中回调到合约中其他的函数中修改状态变量
slot0.unlocked = false;

// 这里也是缓存交易钱的数据，节省 gas
SwapCache memory cache =
    SwapCache({
        liquidityStart: liquidity,
        blockTimestamp: _blockTimestamp(),
        feeProtocol: zeroForOne ? (slot0Start.feeProtocol % 16) : (slot0Start.feeProtocol >> 4)
    });

// 判断是否指定了 tokenIn 的数量
bool exactInput = amountSpecified > 0;

// 保存交易过程中计算所需的中间变量，这些值在交易的步骤中可能会发生变化
SwapState memory state =
    SwapState({
        amountSpecifiedRemaining: amountSpecified,
        amountCalculated: 0,
        sqrtPriceX96: slot0Start.sqrtPriceX96,
        tick: slot0Start.tick,
        feeGrowthGlobalX128: zeroForOne ? feeGrowthGlobal0X128 : feeGrowthGlobal1X128,
        protocolFee: 0,
        liquidity: cache.liquidityStart
    });
...

上面的代码都是交易前的准备工作，实际的交易在一个循环中发生：

// 只要 tokenIn
while (state.amountSpecifiedRemaining != 0 && state.sqrtPriceX96 != sqrtPriceLimitX96) {
    // 交易过程每一次循环的状态变量
    StepComputations memory step;

    // 交易的起始价格
    step.sqrtPriceStartX96 = state.sqrtPriceX96;

    // 通过位图找到下一个可以选的交易价格，这里可能是下一个流动性的边界，也可能还是在本流动性中
    (step.tickNext, step.initialized) = tickBitmap.nextInitializedTickWithinOneWord(
        state.tick,
        tickSpacing,
        zeroForOne
    );

    ...

    // 从 tick index 计算 sqrt(price)
    step.sqrtPriceNextX96 = TickMath.getSqrtRatioAtTick(step.tickNext);

    // 计算当价格到达下一个交易价格时，tokenIn 是否被耗尽，如果被耗尽，则交易结束，还需要重新计算出 tokenIn 耗尽时的价格
    // 如果没被耗尽，那么还需要继续进入下一个循环
    (state.sqrtPriceX96, step.amountIn, step.amountOut, step.feeAmount) = SwapMath.computeSwapStep(
        state.sqrtPriceX96,
        (zeroForOne ? step.sqrtPriceNextX96 < sqrtPriceLimitX96 : step.sqrtPriceNextX96 > sqrtPriceLimitX96)
            ? sqrtPriceLimitX96
            : step.sqrtPriceNextX96,
        state.liquidity,
        state.amountSpecifiedRemaining,
        fee
    );

    // 更新 tokenIn 的余额，以及 tokenOut 数量，注意当指定 tokenIn 的数量进行交易时，这里的 tokenOut 是负数
    if (exactInput) {
        state.amountSpecifiedRemaining -= (step.amountIn + step.feeAmount).toInt256();
        state.amountCalculated = state.amountCalculated.sub(step.amountOut.toInt256());
    } else {
        state.amountSpecifiedRemaining += step.amountOut.toInt256();
        state.amountCalculated = state.amountCalculated.add((step.amountIn + step.feeAmount).toInt256());
    }

    ...

    // 按需决定是否需要更新流动性 L 的值
    if (state.sqrtPriceX96 == step.sqrtPriceNextX96) {
        // 检查 tick index 是否为另一个流动性的边界
        if (step.initialized) {
            int128 liquidityNet =
                ticks.cross(
                    step.tickNext,
                    (zeroForOne ? state.feeGrowthGlobalX128 : feeGrowthGlobal0X128),
                    (zeroForOne ? feeGrowthGlobal1X128 : state.feeGrowthGlobalX128)
                );
            // 根据价格增加/减少，即向左或向右移动，增加/减少相应的流动性
            if (zeroForOne) liquidityNet = -liquidityNet;

            secondsOutside.cross(step.tickNext, tickSpacing, cache.blockTimestamp);

            // 更新流动性
            state.liquidity = LiquidityMath.addDelta(state.liquidity, liquidityNet);
        }

        // 在这里更 tick 的值，使得下一次循环时让 tickBitmap 进入下一个 word 中查询
        state.tick = zeroForOne ? step.tickNext - 1 : step.tickNext;
    } else if (state.sqrtPriceX96 != step.sqrtPriceStartX96) {
        // 如果 tokenIn 被耗尽，那么计算当前价格对应的 tick
        state.tick = TickMath.getTickAtSqrtRatio(state.sqrtPriceX96);
    }
}

上面的代码即交易的主循环，实现思路即以一个 tickBitmap 的 word 为最大单位，在此单位内计算相同流动性区间的交易数值，如果交易没有完成，那么更新流动性的值，进入下一个流动性区间计算，如果 tick index 移动到 word 的边界，那么步进到下一个 word.

关于 tickBitmap 中下一个可用价格 tick index 的查找，在函数 TickBitmap 中实现，这里不做详细描述。

拆分后的交易计算

交易是否能够结束的关键计算在 SwapMath.computeSwapStep 中完成，这里计算了交易是否能在目标价格范围内结束，以及消耗的 tokenIn 和得到的 tokenOut. 这里摘取此函数部分代码进行分析（这里仅摘取 exactIn 时的代码）:

function computeSwapStep(
    uint160 sqrtRatioCurrentX96,
    uint160 sqrtRatioTargetX96,
    uint128 liquidity,
    int256 amountRemaining,
    uint24 feePips
)
    internal
    pure
    returns (
        uint160 sqrtRatioNextX96,
        uint256 amountIn,
        uint256 amountOut,
        uint256 feeAmount
    )
{
    // 判断交易的方向，即价格降低或升高
    bool zeroForOne = sqrtRatioCurrentX96 >= sqrtRatioTargetX96;
    // 判断是否指定了精确的 tokenIn 数量
    bool exactIn = amountRemaining >= 0;
    ...

函数的输入参数是当前价格，目标价格，当前的流动性，以及 tokenIn 的余额。

if (exactIn) {
    // 先将 tokenIn 的余额扣除掉最大所需的手续费
    uint256 amountRemainingLessFee = FullMath.mulDiv(uint256(amountRemaining), 1e6 - feePips, 1e6);
    // 通过公式计算出到达目标价所需要的 tokenIn 数量，这里对 x token 和 y token 计算的公式是不一样的
    amountIn = zeroForOne
        ? SqrtPriceMath.getAmount0Delta(sqrtRatioTargetX96, sqrtRatioCurrentX96, liquidity, true)
        : SqrtPriceMath.getAmount1Delta(sqrtRatioCurrentX96, sqrtRatioTargetX96, liquidity, true);
    // 判断余额是否充足，如果充足，那么这次交易可以到达目标交易价格，否则需要计算出当前 tokenIn 能到达的目标交易价
    if (amountRemainingLessFee >= amountIn) sqrtRatioNextX96 = sqrtRatioTargetX96;
    else
        // 当余额不充足的时候计算能够到达的目标交易价
        sqrtRatioNextX96 = SqrtPriceMath.getNextSqrtPriceFromInput(
            sqrtRatioCurrentX96,
            liquidity,
            amountRemainingLessFee,
            zeroForOne
        );
} else {
    ...
}

这里再次调用了 SqrtPriceMath.getAmount0Delta 或者 SqrtPriceMath.getAmount1Delta 来计算到达目标价是所需的 token 数量。即已知 $\sqrt P_c,\ \sqrt P_n,\ L$，求 $\Delta x$ 和 $\Delta y$. 计算的过程在上一章已经讲过了，运用的公式是：

$$ \Delta x = \Delta {\frac 1{\sqrt P}} \cdot L \\ \Delta y = \Delta {\sqrt P} \cdot L $$

假设交易是输入 x token ，余额为 $x$（预先扣除最大所需的手续费后的余额，以防止手续费不足），在计算得到 $\Delta x$ 后，比较：

当 $x \geq \Delta x$ 时，表示交易可以到达目标价格
当 $x < \Delta x$ 时，表示交易不足以到达目标价格，此时还需要进一步当前余额 $x_remaining$ 全部耗尽时所能够达到的价格

如果 $x < \Delta x$，我们需要计算 x 耗尽时的价格，即已知 $\Delta x,\ \sqrt P_c,\ L$，求 $\sqrt P_n$. 根据：

$$ \Delta x = \Delta {\frac 1{\sqrt P}} \cdot L = \pm({\frac 1{\sqrt P_c} - \frac 1{\sqrt P_n}}) \cdot L $$

得出：

$$ \sqrt {P_n} = \frac {L \sqrt {P_c}}{L \pm \Delta x \sqrt {P_c}} $$

具体上述公式计算仅对通过 x token 余额求出下一个价格的公式进行了推导，如果输入的时 y token，也可以额进行类似的推导。代码中具体的实现已经封装在在 SqrtPriceMath.getNextSqrtPriceFromInput 函数中，这里不再进一步详细解释。我们接着看 computeSwapStep 的剩余步骤：

// 判断是否能够到达目标价
bool max = sqrtRatioTargetX96 == sqrtRatioNextX96;

// get the input/output amounts
if (zeroForOne) {
    // 根据是否到达目标价格，计算 amountIn/amountOut 的值
    amountIn = max && exactIn
        ? amountIn
        : SqrtPriceMath.getAmount0Delta(sqrtRatioNextX96, sqrtRatioCurrentX96, liquidity, true);
    amountOut = max && !exactIn
        ? amountOut
        : SqrtPriceMath.getAmount1Delta(sqrtRatioNextX96, sqrtRatioCurrentX96, liquidity, false);
} else {
    ...
}

// 这里对 Output 进行 cap 是因为前面在计算 amountOut 时，有可能会使用 sqrtRatioNextX96 来进行计算，而 sqrtRatioNextX96
// 可能被 Round 之后导致 sqrt_P 偏大，从而导致计算的 amountOut 偏大
if (!exactIn && amountOut > uint256(-amountRemaining)) {
    amountOut = uint256(-amountRemaining);
}

if (exactIn && sqrtRatioNextX96 != sqrtRatioTargetX96) {
    // 如果没能到达目标价，即交易结束，剩余的 tokenIn 将全部作为手续费
    // 为了不让计算进一步复杂化，这里直接将剩余的 tokenIn 将全部作为手续费
    // 因此会多收取一部分手续费，即按本次交易的最大手续费收取
    feeAmount = uint256(amountRemaining) - amountIn;
} else {
    feeAmount = FullMath.mulDivRoundingUp(amountIn, feePips, 1e6 - feePips);
}

后续的步骤即重新计算了需要支付的手续费用和付出的 tokenIn, tokenOut 数量，这一步的交易就结束了，函数会将手续费，到达的目标价以及 tokenIn, tokenOut 返回。

在进行交易输入/输出的计算时，和流动性的计算一样，也会遇到 rounding 的问题，处理的原则是：

当计算 output 时，使用 RoundDown，保证 pool 不会出现坏账
当计算 input 时，使用 RoundUp，保证 pool 不会出现坏账
当通过 input 计算 $\sqrt P$ 时，如果 $\sqrt P$ 会减少，那么使用 RoundUp，这样可以保证 $\Delta \sqrt P$ 被 RoundDown，在后续计算 output 时不会使 pool 出现坏账。反之如果 $\sqrt P$ 会增大，那么使用 RoundDown
当通过 output 计算 $\sqrt P$ 时，如果 $\sqrt P$ 会减少，那么使用 RoundDown，这样可以保证 $\Delta \sqrt P$ 被 RoundUp，在后续计算 input 时不会使 pool 出现坏账。反之如果 $\sqrt P$ 会增大，那么使用 RoundUp

交易收尾阶段

我们再回到 swap 函数中循环检查条件：

while (state.amountSpecifiedRemaining != 0 && state.sqrtPriceX96 != sqrtPriceLimitX96) {
    ...
}

即通过通过 tokenIn 是否还有余额来判断是否还需要继续循环，进入下一步的进行交易计算。当 tokenIn 全部被耗尽后，交易就结束了。当交易结束后，我们还需要做这些事情：

更新预言机
更新当前交易对的价格 $\sqrt P$，流动性 $L$
更新手续费累计值
扣除用户需要支付的 token

关于手续费，预言机的相关内容，会在其他章节讲解，我们先跳过这部分代码，直接看 swap 函数的末尾：

// 确定最终用户支付的 token 数和得到的 token 数
(amount0, amount1) = zeroForOne == exactInput
    ? (amountSpecified - state.amountSpecifiedRemaining, state.amountCalculated)
    : (state.amountCalculated, amountSpecified - state.amountSpecifiedRemaining);

// 扣除用户需要支付的 token
if (zeroForOne) {
    // 将 tokenOut 支付给用户，前面说过 tokenOut 记录的是负数
    if (amount1 < 0) TransferHelper.safeTransfer(token1, recipient, uint256(-amount1));

    uint256 balance0Before = balance0();
    // 还是通过回调的方式，扣除用户需要支持的 token
    IUniswapV3SwapCallback(msg.sender).uniswapV3SwapCallback(amount0, amount1, data);
    // 校验扣除是否成功
    require(balance0Before.add(uint256(amount0)) <= balance0(), 'IIA');
} else {
    ...
}

// 记录日志
emit Swap(msg.sender, recipient, amount0, amount1, state.sqrtPriceX96, state.tick);
// 解除防止重入的锁
slot0.unlocked = true;
}

这里还是通过回调完成用户支付 token 的费用。因为发送用户 token 是在回调函数之前完成的，因此这个 swap 函数是可以被当作 flash swap 来使用的。

需要注意，如果本次交易是交易路径中的一次中间交易，那么扣除的 token 是从 SwapRouter 中扣除的，交易完成获得的 token 也会发送给 SwapRouter 以便其进行下一步的交易，我们回到 SwapRouter 中的 exactInput 函数：

params.amountIn = exactInputSingle(
    params.amountIn,
    // 这里会判断是否是最后一次交易，当是最后一次交易时，获取的 token 的地址才是用户的指定的地址
    hasPools ? address(this) : params.recipient,
    SwapData({
        path: params.path.getFirstPool(),
        payer: msg.sender
    })
);

再来看一下支付的回调函数：

function uniswapV3SwapCallback(
    int256 amount0Delta,
    int256 amount1Delta,
    bytes calldata _data
) external override {
    SwapData memory data = abi.decode(_data, (SwapData));
    (address tokenIn, address tokenOut, uint24 fee) = data.path.decodeFirstPool();
    CallbackValidation.verifyCallback(factory, tokenIn, tokenOut, fee);

    // 这里有点绕，目的就是判断函数的参数中哪个是本次支付需要支付的代币
    (bool isExactInput, uint256 amountToPay) =
        amount0Delta > 0
            ? (tokenIn < tokenOut, uint256(amount0Delta))
            : (tokenOut < tokenIn, uint256(amount1Delta));
    if (isExactInput) {
        // 调用 pay 函数支付代币
        pay(tokenIn, data.payer, msg.sender, amountToPay);
    } else {
        ...
    }
}

回调完成后，swap 函数会返回本次交易得到的代币数量。exactInput 将判断是否进行下一个路径的交易，直至所有的交易完成，进行输入约束的检查：

require(amountOut >= params.amountOutMinimum, 'Too little received');

如果交易的获得 token 数满足约束，则本次交易结束。

本文仅对 exactInput 这一种交易情况进行了分析，理解了这个交易的整个流程后，就可以触类旁通理解 exactOutput 的交易过程。

交易预计算

（更新于 2021.06.06）

当用户和 uniswap 前端进行交互时，前端需要预先计算出用户输入 token 能够预期得到的 token 数量。

这个功能在 uniswap v2 有非常简单的实现，只需要查询处合约中两个代币的余额就可以完成预计算。

但是在 v3 版本中，由于交易的计算需要使用合约内的 tick 信息，预计算只能由 uniswap v3 pool 合约来完成，但是 pool 合约中的计算函数都是会更改合约状态的 external 函数，那么如何把这个函数当作 view/pure 函数来使用呢？uniswap v3 periphery 仓库中给出了一个非常 tricky 的实现，代码在 contracts/lens/Quoter.sol 中：

function quoteExactInputSingle(
    address tokenIn,
    address tokenOut,
    uint24 fee,
    uint256 amountIn,
    uint160 sqrtPriceLimitX96
) public override returns (uint256 amountOut) {
    bool zeroForOne = tokenIn < tokenOut;

    try
        getPool(tokenIn, tokenOut, fee).swap(  // 调用 pool 合约的 swap 接口来模拟一次真实的交易
            address(this), // address(0) might cause issues with some tokens
            zeroForOne,
            amountIn.toInt256(),
            sqrtPriceLimitX96 == 0
                ? (zeroForOne ? TickMath.MIN_SQRT_RATIO + 1 : TickMath.MAX_SQRT_RATIO - 1)
                : sqrtPriceLimitX96,
            abi.encodePacked(tokenIn, fee, tokenOut)
        )
    {} catch (bytes memory reason) {
        return parseRevertReason(reason);
    }
}

可以看到函数中调用了 getPool(tokenIn, tokenOut, fee).swap()，即 pool 合约的真实交易函数，但是实际上我们并不想让交易发生，这个交易调用必定也会失败，因此合约使用了 try/catch 的方式捕获错误，并且在回调函数中获取到模拟交易的结果，存入内存中。

可以看回调函数：

function uniswapV3SwapCallback(
    int256 amount0Delta,
    int256 amount1Delta,
    bytes memory path
) external view override {
    require(amount0Delta > 0 || amount1Delta > 0); // swaps entirely within 0-liquidity regions are not supported
    (address tokenIn, address tokenOut, uint24 fee) = path.decodeFirstPool();
    CallbackValidation.verifyCallback(factory, tokenIn, tokenOut, fee);

    (bool isExactInput, uint256 amountToPay, uint256 amountReceived) =
        amount0Delta > 0
            ? (tokenIn < tokenOut, uint256(amount0Delta), uint256(-amount1Delta))
            : (tokenOut < tokenIn, uint256(amount1Delta), uint256(-amount0Delta));
    if (isExactInput) {
        assembly {  // 这里代码需要将结果保存在内存中
            let ptr := mload(0x40)  // 0x40 是 solidity 定义的 free memory pointer
            mstore(ptr, amountReceived) // 将结果保存起来
            revert(ptr, 32) // revert 掉交易，并将内存中的数据作为 revert data
        }
    } else {
        // if the cache has been populated, ensure that the full output amount has been received
        if (amountOutCached != 0) require(amountReceived == amountOutCached);
        assembly {
            let ptr := mload(0x40)
            mstore(ptr, amountToPay)
            revert(ptr, 32)
        }
    }
}

这个回调函数主要的作用就是将 swap() 函数计算处的结果保存到内存中，这里使用了 assembly 来访问 solidity 的 free memory pointer，关于 solidity 内存布局，可以参考文档：Layout in Memory.

将结果保存到内存中时候就将交易 revert 掉，然后在 quoteExactInputSingle 中捕获这个错误，并将内存中的信息读取出来，返回给调用者：

/// @dev Parses a revert reason that should contain the numeric quote
function parseRevertReason(bytes memory reason) private pure returns (uint256) {
    if (reason.length != 32) { // swap 函数正常 revert 的情况
        if (reason.length < 68) revert('Unexpected error');
        assembly {
            reason := add(reason, 0x04)
        }
        revert(abi.decode(reason, (string)));
    }
    return abi.decode(reason, (uint256)); // 这里捕获前面回调函数保存在内存中的结果。
}

总结：通过 try/catch 结合回调函数，模拟计算结果，实现了交易预计算的功能，这样 uniswap 前端就能够在获取用户输入后进行交易的预计算了，这部分前端的实现在这里。

Uniswap v3 详解系列

本系列所有文章：

目录